爱因斯坦说：“提出问题比解决问题更重要。”李政道教授曾说过：“最重要的是提出问题。”课堂提问是教师教学的重要手段，是师生互动活动的一种重要形式。只有在问题的提出、分析、解决中，才能逐渐培养学生的思维品质和能力。

在八年级第二学期梯形版块的学习中，遇到这样一道练习题：

例1：已知：如图1，AD∥BC，点E 在线段AB 上，∠ADE=∠CDE，∠DCE=∠ECB。

求证：CD=AD+BC。

这是一道非常典型的“截长补短”思想运用的问题，结论是CD=AD+BC，可考虑用“截长补短法”中的“截长”，即在CD 上截取CF=CB，只要再证DF=DA即可，这就转化为证明两线段相等的问题，从而达到简化问题的目的。

证明：在CD上截取CF=BC，如图2

在△FCE与△BCE中，

∴　△FCE≌△BCE（SAS），

∴　∠2=∠1.

又∵　AD∥BC，

∴　∠ADC+∠BCD=180°，

∴　∠DCE+∠CDE=90°，

∴　∠2+∠3=90°，∠1+∠4=90°，(www.daowen.com)

∴　∠3=∠4.

在△FDE与△ADE中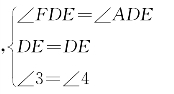

∴　△FDE≌△ADE（ASA）

∴　DF=DA，

∵　CD=DF+CF，

∴　CD=AD+BC.

课堂上讲解和板书此题的解题思路之后，留给学生几分钟思考和订正的时间。这时，思维活跃的A同学举手了，他说：“老师，这道题我还有其他的思路。”我便请A同学走上讲台讲解他的解题思路和方法。他说：“这道题还可以延长DE和CB交于点F，由平行线和角平分线能得到△DCF是等腰三角形。利用等腰三角形三线合一的性质以及全等三角形的性质，也能得到CD=AD+BC。”A同学说完后全班响起了热烈的掌声，A同学回到座位后，我借势提问：“还有没有其他的解题思路？”话音刚落，B同学举手了，“如果能延长DE，那么同样能延长CE，使之与DA的延长线交于点G，这样也能得到结果。”在肯定B同学的解题思路后，我继续提问：“还有没有同学有其他的想法？”教室里一片寂静，有的学生看着黑板上的解题步骤发呆，有的学生埋下头在草稿纸上写着画着，等了几分钟后，我以提问的方式给出提示：“同学们，这道题老师给出的思路是截长补短中的截长，你们能不能从补短的角度去想想看？”又过了几分钟，C同学举起手来，“可以延长DA至点F，使DF=DC，这样能得到△DCE与△DFE全等。通过证明点C、点E、点F三点共线能得到△BCE与△AFE全等，由全等三角形对应边相等就能得到结论。”对C同学的思路进行评析后，我给学生十分钟的时间，让他们重新整理这道题的解题思路和方法。我接着说：“同学们，这道题非常典型，试着将这道题的一个条件和结论交换，又会出现一道新的题目。”接着，我在黑板上板书了由例题改编的一道新题。

例2：已知：如图3，AD∥BC，点E 在线段AB 上，∠ADE=∠CDE，CD=AD+BC.

求证：∠DCE=∠ECB.

学生对这道题表现出了极大的热情，都埋着头，认真思索着。

几分钟后，下课铃声响起了，学生三三两两地聚在一起讨论着这道题的解题思路。学生的反应告诉我，虽然我没有完成既定的教学任务，有一道教学设计中的例题没有时间讲解，但学生的收获却更多，他们强化了“截长补短”的思路，理解三点共线的含义，也明白举一反三的道理。

这节课的问题主要是在非预设的前提下根据课堂动态生成的教学情境随机提出的，这样的即兴提问既激发学生学习数学的兴趣，也尊重学生个体的发展。