吴一波

二次函数作为初中数学的一个重要知识点，在整个初中的数学体系中有着很重要的地位。它是“函数与分析”知识内容中的重点，其中，二次函数背景下的综合题更是学生学习的难点。在如今中考数学“8∶1∶1”的要求下，二次函数处于最后一个“1”的等级之中，是考察学生数学能力的重要题型。而在诸多二次函数背景下的综合题型中，“四点构成等腰梯形”问题是学生学习的一个难点。相较于平行四边形、矩形、直角梯形，等腰梯形无论在分类讨论难度还是数形结合的解法上都对学生提出更高的要求。因此，我将对这一问题进行深入的探索和研究。

所谓的“四点构成等腰梯形”问题，是指已知三个点，求第四个点，使四点构成等腰梯形。这一问题，首先要求学生有十分有条理的分类讨论思想。因为，已知三个点，就可以连接出三条线段。而这三条线段分别应该是等腰梯形的一条底边、一条腰、一条对角线。此时，哪条线段为底，哪条线段为腰，哪条线段为对角线，就需要进行分类讨论。等腰梯形的分类讨论应当从图形的定义出发。等腰梯形，首先是梯形，有一组对边平行，另一组对边不平行的四边形就成为梯形。因此，在等腰梯形的分类讨论过程中，应该从这条定义出发，根据已知的三条线段，令其分别作为梯形的一条底边，从而展开讨论。这一方法适用于所有“四点构成梯形”问题，普通梯形、直角梯形都适用于这一思路。

下面，我将通过两个例题来分析这一题型如何进行分类讨论。

例1：（2016年普陀区中考数学二模卷第24题）在平面直角坐标系x Oy中，二次函数的图像与y轴交于点A，与双曲线有一个公共点B，它的横坐标为4，过点B作直线l平行于x轴，与该二次函数图像交于另一点C，直线AC的截距为-6。求：1.二次函数解析式；2.直线AC的表达式；3.平面内是否存在点D，使A、B、C、D为顶点的四边形是等腰梯形。如果存在，求出D 点坐标；如果不存在，请说明理由。

通过求解，得到A（0，-6）、B（4，2）、C（-6，2）。于是，得到线段AB、BC、AC。此时，应分别以三条线段为底边进行分类。1.线段AB为底边，则点D 应在过点C且平行于AB的直线上。2.线段BC为底边，则点D 应当在过点A 且平行于BC的直线上。3.线段AC为底边，则点D应在过点B，且平行于AC的直线上。通过分析，学生已经初步找出能与A、B、C点构成梯形的点D的位置。接下来，进一步思考如何让这一梯形成为等腰梯形。等腰梯形是指两腰相等的梯形，它在同一底边上的两个底角相等。因此，腰与底边的夹角应大于对角线与底边的夹角，即对角线长应比腰长大。这一性质解决了分类讨论中余下两条线段，哪条线段为腰，哪条线段为对角线的问题，从而能够确定点D 的位置。1.线段AB 为底边时，AC=BC，因此无法构成等腰梯形，所以此情况不成立。2.线段BC为底边时，AC＞AB，因此AB为腰。3.线段AC为底边时，BC＞AB，因此AB为腰。此题所有可能的情况已完全分析清楚，不重不漏。

例2：（2016年闸北区中考数学二模卷第24题）如图，矩形OMPN 的顶点O在原点，M、N 分别在x轴y轴的正半轴上，OM=6，ON=3，反比例函数的图像与PN 交于C，与PM 交于D，过点C作CA⊥x轴于点A，过点D作DB⊥y轴于点B，AC与BD交于点G。求证：1.AB∥CD。2.在平面直角坐标内是否存在点E，使B、C、D、E为顶点，BC为腰的梯形是等腰梯形？若存在，求出点E坐标；若不存在，说明理由。

通过求解，B（0，1）、C（2，3）、D（6，1）。于是，得到线段BC、CD、BD。此题明确指出BC为腰，那么对于底边的讨论就可以简化为两种情况：（1）线段CD 为底边，E点在过点B且平行于CD的直线上；（2）线段BD为底边，E点在过点C且平行于BD的直线上。此题所有可能的情况已完全分析清楚，不重不漏。(www.daowen.com)

在对第四个点所有可能的情况进行完整的分析之后，如何求解出第四个点的坐标是学生遇到的又一个难题。相较于平行四边形、矩形、直角梯形问题，第四个点的坐标并不能快速通过点的平移或是直接转化成几何问题来求解。等腰梯形第四个点的坐标求解需要根据“对边平行”及“两腰相等”这两点，运用代数法进行求解。

在对于第四个点可能出现位置的分析过程中，首先明确第四个点位于哪一条直线上，应先求出直线的解析式，利用一个未知数设出第四个点的坐标。接下来，两腰相等就是边长相等问题，即第四个点所在的腰长应等于另一腰长。用两点间距离公式列出方程，从而求解出未知数，得到第四个点的具体坐标。

在上述例1中，第2种情况中BC为底边，则点D 应当在过点A 且平行于BC的直线上。又BC为平行于x轴的直线，因此直线AD的解析式为y=-6，可设D点坐标为（x，-6）。因为DC=AB，则，从而解得x=-2，另一解为平行四边形，故舍去，则D（-2，-6）。第3种情况，AC为底边，则点D应当在过点B且平行于AC的直线上。先求得直线BD 解析式为，设D 点坐标为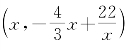。因为DC=AB，则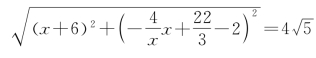，从而解得另一解为平行四边形，故舍去，则

在上述例2中，第1种情况中CD为底边，E点在过点B且平行于CD的直线上。先求得直线BE解析式为，设E点坐标为。因为ED=BC，则，从而解得另一解为平行四边形，故舍去，则第2种情况中，BD 为底边，E点在过点C且平行于BD的直线上。又BD为平行于x轴的直线，因此直线CE的解析式为y=3，可设E点坐标为（x，3）。因为ED=BC，则，从而解得x=4，另一解为平行四边形，故舍去，则E（4，3）。

以上为代数法求解第四个点坐标的具体方法，这种方法对学生解方程能力及计算能力的要求较高，运算量比较大。是否有更加巧妙的方法来帮助学生降低解题难度呢？答案是当所求等腰梯形的底边为水平或者竖直时，可以利用等腰梯形的对称性，采用几何法快速求解出第四个点的坐标。

在上述例1中，第2种情况就符合这种特殊情况。△ABF与△DCE全等，从而CE=BF=4，ED=FA=8，且CE水平，ED 竖直，可以直接得到D 点坐标为（-2，-6）。在上述例2中，第2种情况也符合这种特殊情况。△BCG与△DEF全等，DF=BG=2，EF=CG=2，且DF水平，EF竖直，可以直接得到E点坐标为（4，3）。这种特殊解法必须建立在等腰梯形的底边为水平边或竖直边。因为，只有这样才能将全等三角形的边长直接转化为点的坐标，而当底边不符合这些条件时，无法将边长与点坐标进行快速转化，还是需要利用代数法进行求解。因此，代数法是解等腰梯形问题的通用方法，而数形结合的几何法只能作为辅助手段酌情选用。

通过上述分析，可以发现，“四点构成等腰梯形”问题之所以成为学生学习的一个难点是有道理的。它对于学生如何有序地进行分类讨论，如何巧妙运用数形结合进行点坐标的求解，都提出较高的要求，题目的思维量和计算量也都比较大，确实有必要系统地对其进行研究。同时，如果能够熟练地解决等腰梯形的构成问题，那么平行四边形、矩形、直接梯形的构成问题中，如何有序地分类讨论都可以类比地完成。只要是四边形的构成问题，都应当从定义出发，抓住对边平行的特点，再结合各自特有的性质进行分类讨论。而通过腰长相等熟练地运用代数法求解点坐标，对于平面坐标内两直线平行问题、线段长相等问题、等腰三角形问题也都有着类似的帮助。因此，类比的思想、举一反三的能力在数学学习中时刻都在体现，数学学习应着眼于方法的归纳总结，但更应探究不同问题中数学思想的相同与不同，希望学生能够感悟出其中的道理。