1.创设情境，问题引新

（PPT出示）故事：“国王对国际象棋的发明者的奖励。”

相传古印度国王为奖赏国际象棋的发明者，问他有什么要求，发明者说：“请在棋盘的第1个格子里放上1颗麦粒，在第2个格子里放上2颗麦粒，在第3个格子里放上4颗麦粒，以此类推，每个格子放的麦粒数都是前一个格子里放的麦粒数的2倍，直到放完64个格子为止。请给我足够的粮食来实现上述要求。”

师：你认为国王有能力满足发明者的上述要求吗？

学生思考未答。

师：解决实际问题的基本步骤有哪些？

生：一是仔细阅读题目，找准关键语句，弄清楚求什么，怎么求；二是提取相关数学信息，建立数学模型；三是根据数学模型解决问题。

师：本题的关键语句是哪一句？

生：每个格子放的麦粒数都是前一个格子里放的麦粒数的2倍。

师：本题求什么？如何求？

生：求麦粒的总数，每个格子的麦粒加起来即可，即1+2+22+23+…+263。

师：很好！这个问题的本质是什么呢？

生：这是一个等比数列求和问题。

2.探索研究，推导公式

师：根据刚才的问题，你认为该如何对一般等比数列的前n项和下定义呢？

生：（思索后）类比等差数列的定义，一般地，我们称a1+a2+a3+…+an为等比数列的前n项和，用Sn表示，即Sn=a1+a2+a3+…+an。

师：类比得很好！也即是：Sn=a1+a1q+a1q2+…+a1qn-1，能否用a1,an,n,q来表示Sn呢？

众生沉默思考，不知所措。

师：这个问题比较难，我们先来思考刚才麦粒总数S64=1+2+22+23+…+263，请同学们思考怎么求解。

（学生讨论，教师巡视，参与交流、指导，两分钟后）

生：逐个相加。（有几个学生附和，也有学生提出怎么加。263太大！有的学生一筹莫展）

师：请同学们观察S64=1+2+22+23+…+263①和2S64=2+22+23+…+263+264②，它们的左、右两边式子各有什么相同点？

生：左边都有S64，右边有63项相同项的和。

师：对。那我们能求解S64吗？怎样求？

生：能，用②式减去①式得：S64=2+22+23+…+263+264-（1+2+22+23+…+263）

S64=264-1。

师：大家觉得如何？（学生掌声响起。）(www.daowen.com)

师：那刚才等比数列的Sn=a1+a1q+a1q2+…+a1qn-1怎么求呢？

（众生又沉默，有的不知所措，有的托腮沉思，有的在草稿纸上演算，两分钟后）

生：两边同乘2，再相减。

师：请试一试。（该同学继续演算，也有其他同学演算）

生：不能求出Sn。

师：我们回顾在求解S64中的关键是什么？

生：在求和式子中两边同乘2，即2S64=2+22+23+…+263+264。

师：2是这个数列的什么？

生：公比。

师：两边同乘公比2有何作用？

生：构造S64的方程，63项相同的和。

生：哦，我知道了，两边乘q，得到qSn=a1q+a1q2+a1q3+…+a1qn，应该能推导出Sn。

师：请同学们试试。

生：Sn-qSn=a1+a1q+a1q2+…+a1qn-1-（a1q+a1q2+a1q3+…+a1qn）

（1-q）Sn=a1-a1qn

所以。

师：对吗？

生：不对，如果q=1呢。

师：非常好，两位同学非常棒！合在一起，就是等比数列的求和公式：

师：推导过程的关键在哪儿？

生：在两边同时乘q，使得两式有n-1项完全相同，然后两式错开相减。

师：这叫什么方法呢？大家给它取个名。

生：叫乘公比，错开相减法。

师：大家都叫错位相减法。

师：什么时候用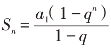？什么时候用？

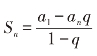生：当已知a1,q,n时用公式，当已知a1,q,an时用公式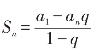，q≠1。