除了采用事件窗口进行回归分析，考虑大宗交易折价幅度和次日开盘价的涨跌幅的时间序列关系，本章仅选取交易次数在60次以上的25支股，如图6−5所示。

图6−5　不同个股在不连续时间上折价幅度和开盘价涨跌幅时间序列关系

表6−4　单位根检验结果

续表

由表6−4可见，Q为统计量，P值为MacKinnon（1996）单侧P值，由于原始数据已经是收益率的形式，因此没有再取对数处理。大宗交易折价率和大宗交易次日开盘价涨跌幅的原始序列经过差分处理之后，符合ADF平稳性要求。

平稳性确定以后，针对以上25支股票，采用Johansen协整检验方法考察大宗交易折价率和次日开盘价涨跌幅的协整关系。检验结果见表6−5。

表6−5　大宗交易折价率和次日开盘价涨跌幅的Johansen检验

续表

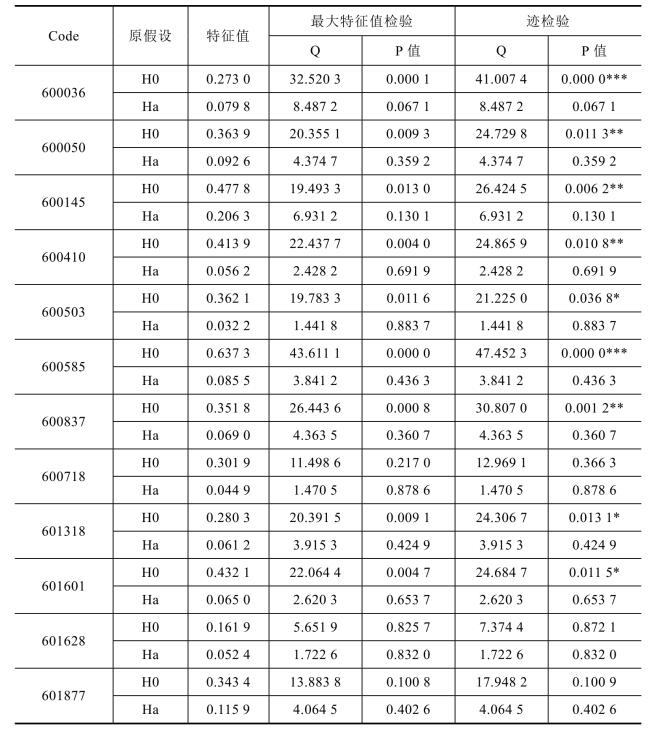
表6−5显示，H0假设为无协整向量，Ha假设为至少有1个协整向量。根据最大特征值检验结果，25支股票中有16支股票的大宗交易折价率和次日开盘价涨跌幅存在协整关系。其中，深圳证券交易所7支，上海证券交易所9支。

针对价格间存在协整关系的16支股票，根据Gonzalo−Granger（1995）的模型，建立大宗交易折价率和次日开盘价涨跌幅的VECM模型采用极大似然法估计参数，调整系数的估计结果见表6−6。(www.daowen.com)

表6−6　Gonzalo-Granger模型调整系数估计结果

表6−6中，大宗交易折价率的调整系数为，开盘价涨跌幅的调整系数为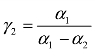。大宗交易折价率的调整系数大多是显著的，而次日开盘价涨跌幅的大部分调整系数不显著。这表明，大宗交易价格向均衡调整的速度相对较快，大宗交易折价率的发现功能比次日开盘价涨跌幅的发现功能弱，这与本章假设6−2不符。

这是所有16支股票的统计结果，但考虑在不同的特质风险股票中调整系数的大小可能不同，做出调节系数与特质风险的相关图，如图6−6所示。

图6−6　调节系数与特质风险的相关矩阵图

由图6−6可以发现，特质风险与调节系数存在显著的负相关关系，说明尽管整体大宗交易市场发现功能较弱，但相对而言，特质风险越高，价格发现功能却相对较强。

以VECM模型为基础，根据Hasbrouck（1995）模型，采用永久短暂模型和信息份额模型分析大宗交易折价率和次日开盘价涨跌幅的价格发现功能，共同因子权重和信息份额的结果见表6−7。

表6−7　Hasbrouck模型大宗交易价格发现贡献结果

续表

从共同因子权重来看，大宗交易折价率的平均共同因子权重小于次日开盘价涨跌幅的平均共同因子权重。16支股票中有5支股票的大宗交易共同因子权重大于正常交易共同因子权重，占比31.25％。从信息份额来看，16支股票中也有5支股票大宗交易折价率的平均信息份额大于次日开盘价涨跌幅的平均信息份额。16支股票的平均值显示，大宗交易折价率的信息份额小于次日开盘价涨跌幅的信息份额。信息份额模型和永久短暂模型得到了相似的结果，表明整体大宗交易折价率的价格发现贡献相对较小，价格发现功能弱。

同样，为精确看出是否不同特质风险股票的表现不同，分析共同因子权重和信息份额权重分别与股票特质风险的相关度，相关系数结果显示为0.67和0.52，说明共同因子权重和信息份额权重占比较高的股票，其平均特质风险较高。这同样说明，尽管大宗交易的价格发现功能较为微弱，但这种微弱性与特质风险存在显著的相关关系，这说明特质风险越高，则价格发现功能相对越强。