1.计算大宗折价率和个股在大宗交易前不同时间的累计超额收益率

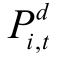定义大宗折价率，其中为大宗交易发生价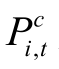，为大宗交易发生日该股在场内市场的收盘价^[2]。由于大宗交易基本都为折价交易，所以计算出的Pp％Δ全部为负数，如表5−1大宗交易折价率的描述性统计所示。

表5−1　大宗交易成交价折价率的描述性统计（2008.12—2012.12）

由表5−1可以发现，大宗交易样本中一共有17 997个观测值，平均折价率为6.62％，折价率的标准差为3.35％，最大折价幅度为29.8％，最小折价幅度几乎为零。

大宗交易的折价幅度可能和个股的特质风险存在一定的关联，图5−1为做出的大宗交易折价率与特质风险的相关关系矩阵图。

在图5−1中，由于数据样本较大，特质风险和大宗交易折价率的数据频率存在一定差异，前者为每个个股在每个月的月度数据，后者为每笔大宗交易在某日发生的日度数据。尽管不能看出大宗交易折价率与特质风险的严格单调相关关系，但二者的分布主要集中在负向关系的区域。当然，这也说明大宗交易折价率与特质风险不存在明确的共线性关系。

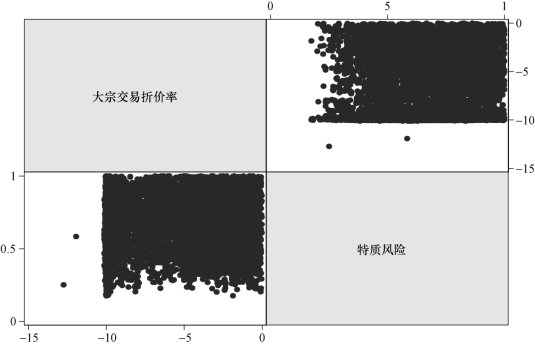
图5−1　大宗交易折价率与特质风险的相关关系矩阵图(www.daowen.com)

2.建立回归方程组

根据5.2节理论模型和研究假设，尝试建立特质风险与大宗交易折价率之间的回归模型。根据第4章的计算结果，每一笔发生的大宗交易都有唯一对应的。同时，也按照第4章的步骤加入3个控制变量。由于经典文献中常常认定大宗交易是流动性需求引致，流动性溢价导致了大宗交易的折价，因此增加个股换手率作为流动性水平的代理变量，设定为hshlvi,t；增加股票流通市值对数作为公司发展阶段和公司规模的代理变量，设定为ltgbi,t；增加市净率指标，作为公司公开信息中滞后一个季度的经营信息变量，设定为shjlvi,t。除此之外，根据第2章的文献回顾，由于被交易个股在大宗交易前价格的走势可能惯性地影响大宗交易的定价，使得大宗交易的价格受到交易前个股的累计超额收益率的影响。为此，也将个股大宗交易前的超额收益率作为控制变量纳入实证模型中。根据大宗交易的事件时间窗口，把交易前90天至交易发生日的不同时间点的累计超额收益率作为控制变量纳入研究，看大宗交易前的较长时间区间里，特质风险对大宗交易定价在时间序列上的影响。

个股在大宗交易事件窗口期的超额收益率计算如下：

设AR−bi,60，AR−bi,59，…，AR−bi,1为大宗交易发生前60天、前59天直至前1天的超额收益率。AR−bi,t的计算方式为：设发生大宗交易的当日，即t=0日为事件日，根据余晓明（2010）的大宗交易事件统计窗口，设观察大宗交易发生前估计窗口为［−90，−60］，大宗交易发生事件窗口为［−60，+30］，估计窗口中，根据CAPM模型得出αi和βi，再利用αi和βi在事件区间［−60，30］内求出期望收益率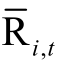，再用实际收益率减去事件期的预期收益率得到超额收益率AR−bi，t=Ryi，t−Iyi,t，再对超额收益率累加得到CARi,t。

综合上述变量的回归方程组5−1如下：

ΔPp％i，t=ai，t+Xbi,t+ui,t，其中

方程组5−1　个股特质风险引起大宗交易折价定价（逐步添加控制变量）