根据Bolton（1998）和Seppi（1990）的模型，设大宗交易市场的交易者为买者和卖者，卖者知道的信息比买者多。设卖者的交易品分为信息含量较少、特质风险不高的股票和信息含量较多、特质风险较高的股票，前者的占比为η，后者的占比为1−η。设被交易的股票价值为υ，由前述第3章交易制度可知，大宗交易的价格可以基于场内价格上下浮动一定比例，设浮动后的下限为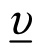，浮动后的上限为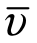，而股票的价值均匀分布在区间［υ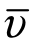，］，则股票价值的期望值为。

设大宗交易的买者不清楚卖者拥有的股票信息，面对所购买的股票的不确定性，购买的价格为p。根据5.1节Grossman（1990）的模型，对于信息含量较多、特质风险较高的股票，期望和意愿卖出的条件是p≥υ。

因此，对于信息含量较少、特质风险不高的股票，在市场价格为p时，愿意成交的概率是100％，而对于信息含量较多、特质风险较高的股票，在市场价格为p时，愿意成交的概率是prob{υ≤p}。在υ服从均匀分布的情形下，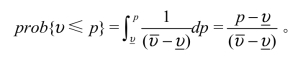

因此，当大宗交易买者出价p时，实现成交的概率λ为：

此时，大宗交易买者在出价为p时，被交易的大宗股票的真实期望值E（υ）为：

根据这一期望值，大宗交易买入者所出的价格p应等于这一期望值才能实现买卖的成交，实现市场的均衡和最优。

对此式求解，可得到价格p的表达式为：

并可得到关于p的二元一次方程组，进而求得p的解。

由（式子5.2.5）可知，大宗交易的成交价格主要由信息含量较少、特质风险不高的股票和信息含量较多、特质风险较高股票的比例、大宗交易最大下浮价格、最大上浮价格这3个因素决定。(www.daowen.com)

对上式中η求一阶导数可得：

经过化简，在条件下，得p′＞0，说明大宗交易价格p是信息含量较少、特质风险不高的股票η（或者信息含量较多、特质风险较高的股票1-η）占比的增函数（减函数）。这说明，当有一定程度信息含量较多、特质风险较高的股票，大宗交易买入者由于信息不对称的因素，会降低大宗交易价格p。

在理想状态下，

因此，当0＜η＜1时，大宗交易的成交价。当由于被交易的股票特质风险较大，造成较大的信息不对称，大宗交易卖出的信息含量较多、特质风险较高股票占比增加时，大宗交易成交价越低，即大宗交易成交价相对于场内市场价表现出一定的折价性。

根据上述模型，提出如下研究命题：

命题5−1：大宗交易发生时，当市场中卖出的股票存在信息含量较多、特质风险较高股票η时，卖者可能对买者的不确定性支付一个溢价，也就是给予买者风险补偿，使得大宗交易的价格p可能表现为折价交易，即。

命题5−2：特质风险与折价幅度存在负向关系，即特质风险（1−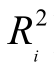）越大，折价幅度可能越大。随着特质风险的变化，折价的幅度出现相应的变化。