除了进行截面分析以外，为了从48个月中看出整体股票市场是否在面板维度表现出特质风险对大宗交易发生的决定效果，对整体数据作面板回归。

首先建立面板回归方程组4−4，Ui，t=　ai，t+Xbi，t+ui,t，其中：

方程组4−4　个股特质风险决定大宗交易的发生（面板分析）

在X矩阵中，one rsqr1为CAPM模型求出的1−R2，hshlv依然为股票的换手率，ltgb依然为股票的流通市值对数，shjlv为股票的市净率，one rsqr1 hshlv为特质风险与换手率的交叉项（1−R2）×hshlv，one rsqr1 ltgb为特质风险与市值数的交叉项（1−R2）×ltgb，one rsqr1 shjlv为　特质　　险与市净率的交叉项（1−R2）×shjlv。回归结果如表4−5所示。

表4−5　个股特质风险决定大宗交易的发生（逐步添加控制变量的面板结果）

续表注：T值全部为绝对值

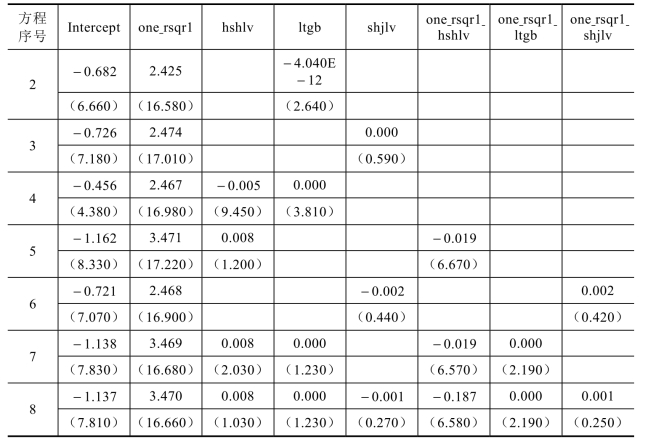
在表4−5中，逐步添加了不同的控制变量，结果如下：

（1）从方程1到方程8，所有的1−R2系数都为正且全部在2.4以上，说明就平均水平而言，特质风险每增加1％，股票的大宗交易量的发生增加2.4％以上，且这一影响都非常显著，t值全部大于16.6。

（2）换手率与大宗交易发生量大部分是负向关系，但系数非常小，仅仅为−0.004，说明股票的换手率增加时，股票的大宗交易发生量会降低，这说明一旦股票流动性变好，市场将不愿意选择进行大宗交易。这一结论支持了文献回顾中的流动性驱动大宗交易发生的理论。随着控制变量的加入，影响关系转为正向，但系数值很小且不再显著，说明流动性需求促使大宗交易的发生，这一影响非常微弱。添加了与特质风险的交叉项后，发现换手率越高的股票，特质风险对大宗交易发生的影响会削弱，说明同样特质风险大小的股票，流动性越好时，大宗交易发生量相对降低。

（3）股票的流通市值对大宗交易的影响几乎为零，并不成正向关系，也不太显著，说明股票市值的大小不太会显著影响大宗交易。通过交叉项可以发现，市值增加，特质风险对大宗交易的影响略微加大。

（4）股票的市净率对特质风险引起的大宗交易变化都几乎无影响。

除了考虑基本的线性回归以外，也采用固定效应（FE）模型Yit=ai+Xitb+uit或随机效应（RE）模型Yit=Xitb+（ai+εit）进行实证检验。其中Yi,t为大宗交易量Ui,t，Xi,t为（1−R2）等解释变量。(www.daowen.com)

首先，不添加控制变量时，对是否选择固定效应还是随机效应模型进行Hausman检验，结果如表4−6所示。

表4−6　Hausman检验（未添加控制变量）

其中b=consistent under Ho and Ha，B=inconsistent under Ha。可以发现，不添加控制变量的Hausman检验拒绝随机模型。再次，添加相关控制变量，继续进行Hausman检验，得到的结果如表4−7所示。

表4−7　Hausman检验（添加控制变量）

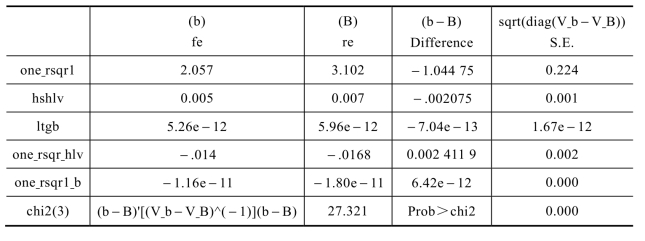
同样发现，Hausman检验拒绝随机效应，因此选用固定效应回归模型Uit=ai+Xitb+uit进行实证，其Xit依然为方程组4−4中的矩阵。回归结果如表4−8所示。

表4−8　特质风险对大宗交易发生量的固定效应模型回归

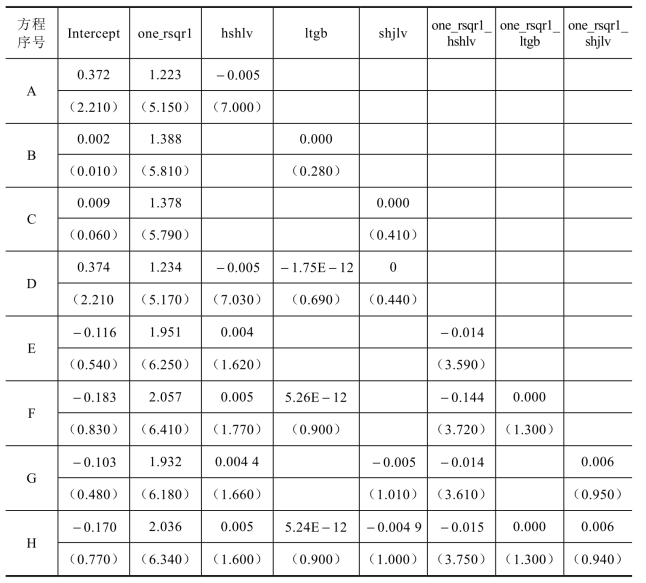
注：T值全部为绝对值

由表4−8可以发现，采用固定效应模型的回归结果中，特质风险对大宗交易发生量的决定系数依然全部为正，且全部显著。同时，逐步添加了不同的控制变量后，从方程A到方程H，换手率依然与大宗交易量占比是负向关系，系数依然非常小，同时越高换手率的股票，特质风险对大宗交易发生的影响越弱。而且，股票的流通市值和市净率对大宗交易的影响都不显著。

如果采用FAMA−FRENCH方法得出特质风险1−R2后，再用上述面板模型回归，得到大宗交易与特质风险one rsqr2的关系如表4−9所示。

表4−9　特质风险对大宗交易影响（FAMA−FRENCH面板方法）

从表4−9中可以看出，特质风险决定大宗交易的发生，这一影响依然为正，且非常显著。这进一步说明了特质风险对大宗交易的显著决定作用，论证了所有的命题。