除了把整体样本作为面板数据进行Logit分析，也可以在每个月度分析所有股票的特质风险对大宗交易的影响，采用每个月度对所有个股进行截面回归的方式。

（1）先建立简单的回归方程，，其中Ui,t=，如果在当月大宗交易数据没有发生，则取值为0，否则将该月的月度大宗成交额求和加入。整体回归方程组表示如下：

方程组4−2　每个月度大宗交易发生额对所有个股特质风险的截面回归方程组

此方程组的目的是检验特质风险是否决定了大宗交易的发生，从而回答大宗交易为什么存在这一问题。按照上述回归方程组，得到的截面结果如表4−4所示。

表4−4　对特质风险决定大宗交易的存在按月度回归分析（截面分析）

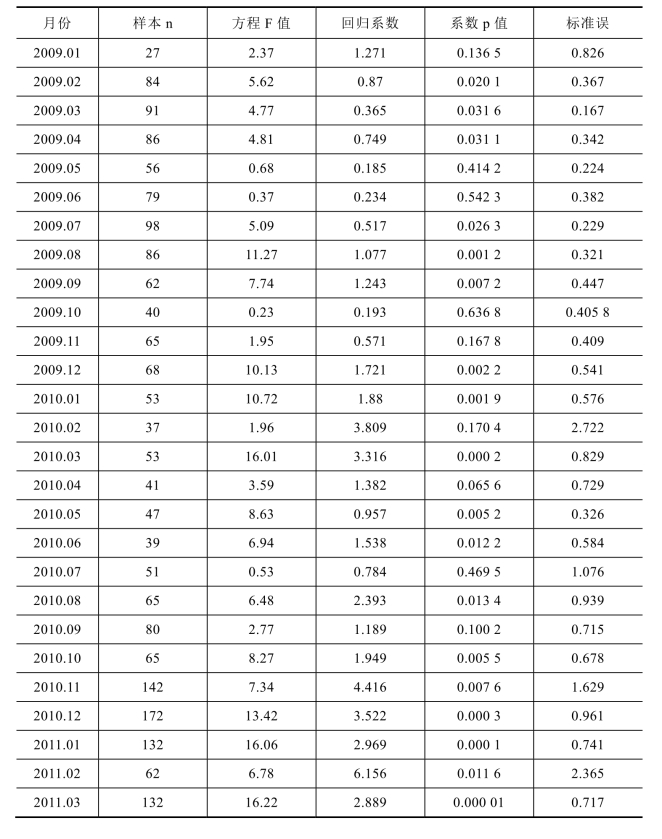
续表

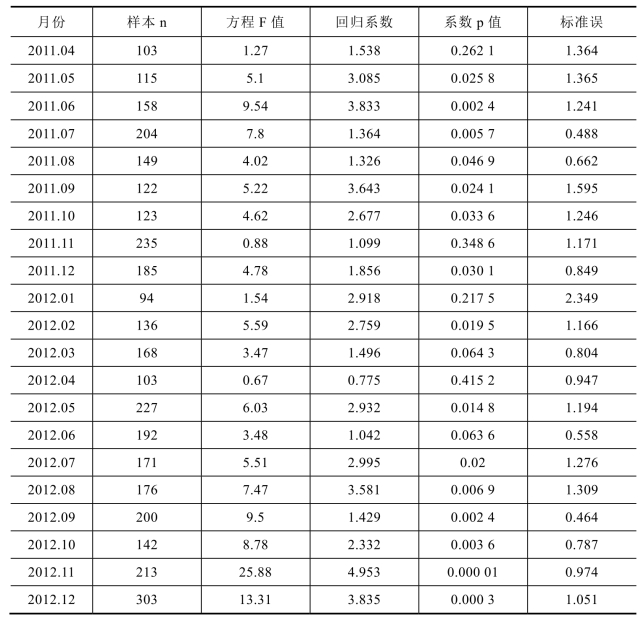
由表4−4可以发现，从2009年1月至2012年12月的48个月内，特质风险对大宗交易发生量的决定是显著的，说明特质风险决定大宗交易的存在，特质风险作用是显著的。

随着时间的推移，发生大宗交易的股票数量呈现递增趋势，从每月27个股票样本增加至每月303个样本。逐月对股票个体的截面回归显示，股票的特质风险对大宗交易量的影响系数全部为正值，分布在0.18至6.15之间，说明特质风险每增加1％，股票的大宗交易发生量增加0.18％～6.15％，各月度的影响系数大小如图4−3所示。

图4−3　特质风险影响大宗交易存在的决定系数（各月度回归系数）

每月的系数显著性都较高，整体48个月中，按0.01显著性水平计算，显著的月数占总月份的比重为57.5％，按照显著性水平为0.05计算，显著的月份占总月份比重为78.75％，如果按显著性水平为0.1计算，则显著的月份占总月份比重高达88％，如果再按显著性水平为0.2计算，则高达92％。各月度的显著性水平p值分布如图4−4所示。(www.daowen.com)

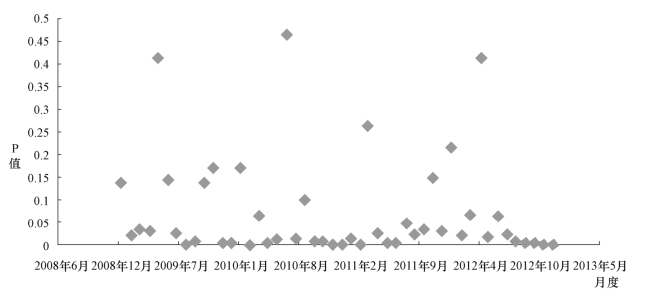
图4−4　特质风险决定大宗交易存在的决定系数的p值（各月度）

图4−4中，按月分析，在每一月里特质风险影响大宗交易存在的决定系数的p值都较小，除了个别特殊月份，这些特殊月份主要集中在每年的季度报告或者年报披露时间段。可能这些特殊月份由于是信息披露时间，公司的信息更加透明，公司特有特定信息减少，因此特质风险降低，特质风险的影响力度下降。

（2）为更清晰地比较特质风险对大宗交易量发生的决定作用，添加第2章文献回顾中提及的其他控制变量，建立新的方程组4−3如下：

其中i=1,2,3,....5 502

方程组4−3　每个月度对所有个股进行的截面回归方程组（添加控制变量）

回归得到特质风险对大宗交易存在的决定系数γi,t，其显著性系数如图4−5所示。

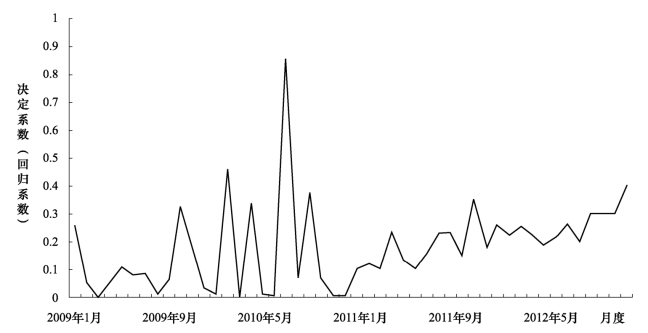
图4−5　特质风险影响大宗交易存在的决定系数（添加控制变量，按月）

由图4−5可见，添加了各个控制变量之后，特质风险对决定大宗交易存在的决定系数依然全部为正数，说明特质风险在发挥影响和决定作用。由于解释变量中加入了取完对数后的变量，这些决定系数的值比不添加控制变量时更小，大部分在1.0之下。而且，按照时间序列，2010年以后该决定系数的走势开始变得相对平滑，且含有向上稳步变大的趋势。

图4−6中，特质风险影响大宗交易存在的决定系数依然较为显著，整体48个月中，按0.01显著性水平计算，显著的月数占总月份比重为59.6％，按照显著性水平为0.05计算，显著的月份占总月份比重为74.2％，如果按显著性水平为0.1计算，则显著的月份占总月份比重高达83％，如果再按显著性水平为0.2计算，则高达94％。

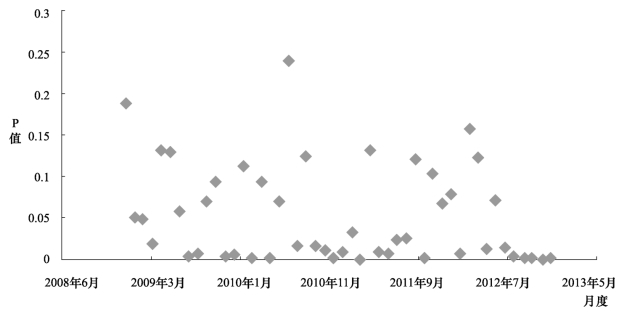
图4−6　特质风险影响大宗交易存在的决定系数的p值（添加控制变量，按月）