在上述Grossman（1992）模型的基础上，根据Chae（2004）交易规模与信息量模型与 Alzahrani（2009）大宗交易价格和订单规模的模型，设场内市场股票的价格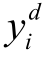与订单规模Xi的关系为：

其中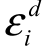为随机误差项。

而大宗交易市场的价格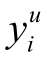，根据Lin（1995）的模型，基于量大批发性或者流动性需求，交易者愿意为价格实施一个折扣λi，同时根据Seppi（1990）的模型，交易者愿意博弈给出一个特有的信息量ζi，那么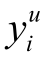与订单规模Xi的关系可以表示为：

则有大宗交易价格为：

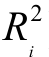根据Campbell（2001）和Grossman（1992）的模型，若令，，其中（1−）为不可观测股票特质风险，则有：

设Ωi为公开信息集，Wi为成本差异因素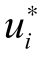，为某支股票选择不去场内市场交易而去大宗交易市场交易占比差异，则有：

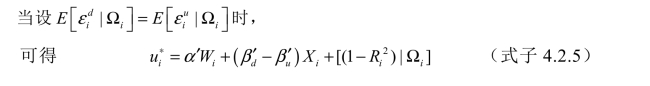
式子4.2.5说明交易者选择在大宗市场交易还是在场内市场交易，取决于四方面的内容：一是交易前的公开信息集；二是成本差异；三是订单规模量；四是股票的特质风险。(www.daowen.com)

若令Zi=（Wi,Xi），令θi=−k（1−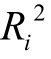）|Ωi，则有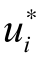=γ′Zi+θi形式。

依据图2−2，在特质风险较高时，买方和卖方的信息不对称程度越高，交易双方降低信息不对称程度的需求越强烈，越愿意选择议价交易。设交易行为的发生服从正态分布，利用标准正态密度函数φ和累计正态密度函数Φ，假设一个订单选择去大宗交易市场还是选择去场内交易市场服从0−1分布，即，可得：

大宗交易市场价格的表达式为：

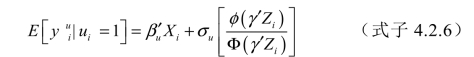
其中σu是θi与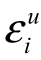的协方差，。

因此，大宗交易市场价格的表达式为：

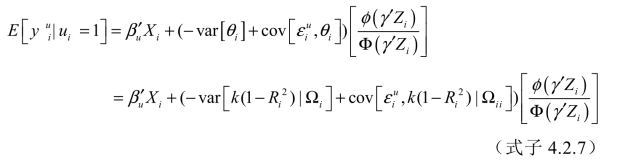
同理，场内市场价格的表达式为：

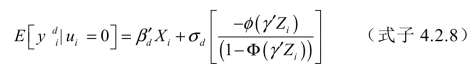
其中。

因此，根据上述理论和式子4.2.5，提出本章的研究命题：

命题4−1：在场内场外市场不存在明显成本Ω差异，订单规模差异不大时，特质风险（1−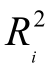）越高，信息不对称程度越高，议价需求越强烈，股票交易越容易在大宗交易市场发生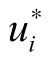，越大。

命题4−2：伴随着特质风险（1−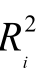）的增加，信息含量增加，持有该股票需要被议价的需求增加，即通过大宗交易方式发生的交易量增加，大宗交易发生量上升。