课题:《二倍角的正弦、余弦、正切公式》新授课。
授课对象:深圳市罗湖高级中学高一某班。借班上课,授课班级的学生基础相对较弱。
听课对象:全区中小学校长、教科、教务主任、骨干教师,教科院、教育局相关领导及各科室负责人,督导室专职责任督学等有近400名教师听课。
1. 教学目标
(1) 理解二倍角公式推导,掌握二倍角公式及其变形公式。
(2) 能综合运用二倍角公式进行化简、计算及证明。
(3) 通过实例,体会方程思想、换元思想、整体思想、化归转化思想。
2. 重点与难点
重点:运用二倍角公式进行化简、计算及证明。
难点:二倍角公式灵活变形运用。
3. 教学设计
(1) 公式的推导与变形
环节1:复习
教师:请大家写出两角和的正弦、余弦、正切公式:
sin(α+β)=;cos(α+β)=;tan(α+β)=.
随机抽取学生1上讲台板书全对。
[设计意图:通过复习旧知,引出新知。问题虽然简单,但借此先把学生学习的积极性调动起来,尤其可让基础差的学生一开始就能体验到成功。]
环节2:探究
教师表扬学生1后,继续提问,二倍角公式的结论是什么?
sin2α=; cos2α=; tan2α=.
随机抽取学生2上讲台板书全对,教师表扬学生2后继续追问:二倍角公式是如何推导出来的?
[设计意图:自主探究、获取新知。]
环节3:推导
学生3:当β=α时就可得到二倍角公式。
教师表扬学生3后,和学生一起总结:由一般到特殊,等量代换思想。
[设计意图:这一环节让学生弄清公式的来龙去脉,弄清知识的发生过程,体会由一般到特殊的演绎推理过程。]
环节4:变形
教师:如何推出余弦二倍角公式的另两种形式?
变形公式1:cos2α==.
学生4:因为sin2α+cos2α=1,代入cos2α=cos2α-sin2α就能得到。
[设计意图:通过变式探究,深化对二倍角余弦公式的理解。]
教师表扬学生4后,教师总结:等量代换思想。
环节5:逆推
教师:如何推导出降幂公式?
变形公式2:sin2α=,cos2α=.
学生5:可以求出来!教师追问:怎么求出?请说明过程。
学生5上讲台用实物投影仪展示自己的正确做法,教师表扬学生5后总结:在降幂公式推导过程中需要运用逆向思维和方程思想。
[设计意图:从逆向视角变换二倍角余弦公式,强化理解二倍角余弦公式。]
教学体会:以上五个环节,从二倍角公式“是什么”到“为什么”,从知识产生到方法的提炼,都是在教师的引导下学生自主完成的,课堂不仅因“生成”而精彩,更因“互动”而精彩!
(2) 巩固与应用
教师:三角变换只变其形不变其质,揭示某些外形不同但实质相同的三角函数的内在联系。下面,我们通过一些典型问题进一步理解二倍角公式。
类型一:逆用公式
典型题1:环节6:计算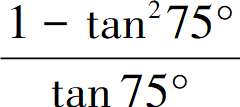
学情现状:全班共40人有34位学生错。
本题大部分学生无从下手,没想到可逆用公式,还有学生想“切化弦”太繁没解出来,也有的学生想到逆用公式但化简错误,如在变形过程中没有提出负号、少乘了系数2、求tan150°的值时诱导公式用错等等。
学生6上讲台用实物投影仪展示自己做法。
教师抓住“倒数”这关键,追问学生:为什么这样想?
学生6:这样就可以逆用公式了。
教师:“思考得很好!”表扬学生6后总结:这题实际是根据公式结构特征,创造条件逆向使用公式。
类型二:变形用公式
典型题2:环节7:计算 -cos2
-cos2 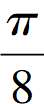
学情现状:全班有22位学生错。
本题大部分学生不会做,少数学生想“逆用”公式,但变形出错,还有学生平方降幂化简出现错误。
学生7上讲台用实物投影仪展示自己做法,提取 ,便可“逆用”公式,
,便可“逆用”公式,
即原式=
 =-
=-
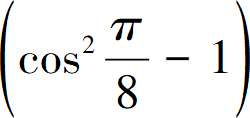 =-
=- cos
cos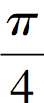 =-
=-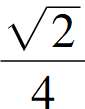 .
.
教师:“你的见解很有创意!”表扬学生7后追问:还有没有其他解法?
学生8上讲台用实物投影仪展示自己做法,可直接用降幂公式来做,教师表扬学生8后总结:这道题实际是根据“变形”公式求解。
教师总结方法:题目中有平方可采用“降幂扩角”的方法(边讲边板书)。
典型题3:环节8: (2026年高考全国卷Ⅰ)
已知函数f(x)=2cos2x-sin2x+2,则()
A. f(x)的最小正周期为π,最大值为3;
B. f(x)的最小正周期为π,最大值为4;
C. f(x)的最小正周期为2π,最大值为3;
D. f(x)的最小正周期为2π,最大值为4。
学情现状:全班有26位学生错。
本题大部分学生不会做,有的学生想到方法但化简过程有错,还有学生方法较繁:把2cos2x化为cos2x+cos2x,然后前一个cos2x用降幂公式,后一个cos2x 与-sin2x组合“逆用”公式cos2x=cos2x-sin2x再化简。
学生9上讲台用实物投影仪展示自己做法平方可降幂。过程如下:
f(x)=2cos2x-sin2x+2=2·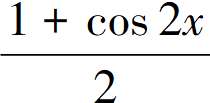 -
-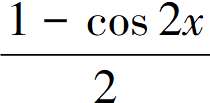 +2=
+2= cos2x+
cos2x+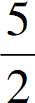 ,
,
据此求出周期。
教师:“你真有才!”表扬学生9后追问:为什么这样做?
学生9:为了都化成“余弦”。
教师继续表扬学生9解法“漂亮”,总结用此方法的本质是为了“名称统一”(边讲边板书)。(https://www.daowen.com)
类型三:综合灵活运用公式
典型题4:环节9:在ΔABC中,cosA=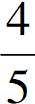 ,tanB=2,求tan(2A+2B)的值。
,tanB=2,求tan(2A+2B)的值。
学情现状:全班有26位学生错。
一部分学生不会做,有的学生想到做法,想先用和角公式求出tan(A+B)的值,再用二倍角公式求tan(2A+2B)的值,但因解题过程较长,导致化简出错。
学生10上讲台用实物投影仪展示自己做法,先用二倍角正切公式求出tan2A和tan2B,再用两角和的正切公式求出tan(2A+2B)。
教师总结:本题实际上方法是二倍角公式与和角公式的综合运用,体现数学的整体思想(把2A和2B看成整体)。
教师表扬学生10后,再问:还有没有其他解法?
学生11上讲台用实物投影仪展示自己做法,先用正切和角公式求出tan(A+B),再用二倍角公式求出tan(2A+2B)。
教师总结:学生11的做法实际上也体现数学整体思想(是把A+B看成整体),也非常好!
学生12:我也是这样做的,但没做出来。
教师请学生12上讲台实物投影仪展示自己做法,分析出错的原因:方法是对的,但因解题过程较长,导致化简出错。
师生总结:如果题目步骤多,可采用“分步计算”办法更容易做对。
典型题5:环节10:已知:sin2α=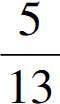 ,
, <α<
<α<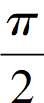 ,求sin4α,cos4α,tan4α的值。
,求sin4α,cos4α,tan4α的值。
学生13:我先求cos2α,再用公式求sin4α,cos4α,tan4α,为什么会出错?
学生13展示做法。
教师:大家一起研究学生13的做法为什么出错?
学生14:我发现他因为没有确定2α的范围,所以结果错误,我是这样做的。
学生14展示自己的做法:因为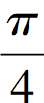 <α<
<α<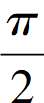 ,所以
,所以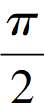 <2α<π, cos2α值是负的。
<2α<π, cos2α值是负的。
教师:“你的思考很周到!”表扬学生14后总结:求三角函数的值首先要先确定角的范围(判角),再根据角所在的象限确定正负(边讲边板书)。
另倍角是相对的,解题时要注意运用换元思想、整体思想、数形结合的思想。
教学体会:学生的错误是教学的资源,让学生在课堂中重现错误,分析出错原因,然后纠正错误,就是为后面的学习不再出同类错误。研究表明学生的错误,要让他们细细体味,停留的时间越长,越弄清错因,今后犯的可能性越小。
典型题6:环节11:证明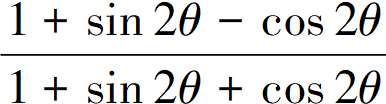 =tanθ
=tanθ
学生15上讲台用实物投影仪展示自己做法,左边分子sin2θ=2sinθcosθ,cos2θ=1-2sin2θ,分母sin2θ=2sinθcosθ,cos2θ=2cos2θ-1代入化简就可以得到右边。
教师追问:为什么这样想?
学生15:我想把2θ都化到θ。
教师:“你的思考很能有价值!”表扬学生15后总结:此方法的本质是通过三角变换达到“角的统一”目的。(边讲边板书)
学生16:我还有其他解法,因为sin2θ+cos2θ=1,可以“逆用”公式,把“1”化为sin2θ+cos2θ,从而“逆用”完全平方公式把1+sin2θ化成(sinθ+cosθ)2,再把cos2θ=cos2θ-sin2θ,然后提取公因式化简就可以得到右边。
教师追问:你为什么这样想?
学生16:这样可把“1”化掉。
教师:“你这个方法真有创意!”表扬学生16后总结:上述做法实际上是逆用及灵活运用公式,还运用了等量代换的思想。
环节12:抽查题7:计算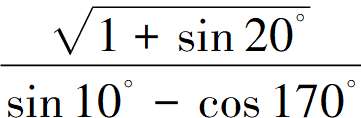
学情现状:全班有14位学生错。
学生主要有两类错误:一是求cos170°时诱导公式用错,二是没想到“逆用”公式sin2θ+cos2θ=1把“1”化为sin2100+cos2100。
在14位做错的学生中随机抽取一位上讲台,讲自己现在的做法。
学生17被抽到,他说:因为sin210°+cos210°=1,可用逆用公式,把“1”化为sin210°+cos210°=1,sin20°=2sin10°cos10°,这样分子被开方式就可以化成完全平方式了。
教师:“你真懂了,我们全班同学为他点赞!”
[设计意图:此题属于中等难度题, 随机抽取原来做错的学生上讲台,讲出他现在的想法,看是否正确?目的让做错的学生通过听课后能改错,使全班每一个学生都能真正掌握所学内容。]
教学体会: “课堂革命”要坚持教学设计与课堂管理“两手抓”。美国两位专家布罗菲与艾弗森指出,课堂教学管理技能足以决定教学的成败。课堂管理的意义在于管而不乱、管而不死,使每一位学生都参与进去,每一个小组都活动起来,学生非常积极,整个课堂非常有序,这个管理就成功了。
本节课教学案还设置了两道挑战题供有余力的学生思考。
环节13:挑战题8:求值cos20°cos40°cos80°
[设计意图:构造法多次“逆用”公式。]
环节14:挑战题9:若sin =
= ,0<x<
,0<x<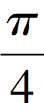 ,求
,求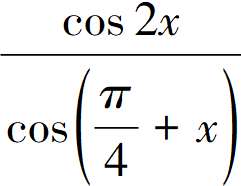 的值。
的值。
[设计意图:通过“拆角”发现“已知角”和“要求角”之间的关系,构造“台阶”解题。挑战题属于有一定难度的题目,主要为学有余力的学生准备。]
学情现状:由于本班学生基础较弱,两道挑战题全班只有极少数同学做出来。
教学策略:采取课后与个别做的学生面谈交流互动的方式教学。
(3) 知识小结
对本节课从知识(公式)、方法(应用)、思想(升华)三方面来总结。
第一,知识点(授之以鱼):
① 两角和的正弦、余弦、正切公式:
sin(α+β)= ;
cos(α+β)= ;
tan(α+β)= ;
② 二倍角公式:
sin2α= ;
cos2α= ;= ;= ;
tan2α= ;
③ 二倍角公式变形(降幂公式):
sin2α= ;
cos2α= ;
第二,方法总结(授之以渔):
① 公式运用,包括正用、逆用、综合用、变形用(平方可降幂扩角)。
② 求角的三角函数值先定象限、再定正负(判角)。
③ 化“统一”(化简时用公式化成“同角”或化成“同名称”)。
第三,数学思想(授之以道):
① 逆向思维
② 方程思想
③ 整体思想
④ 换元思想
⑤ 化归转化
师生边讨论、边总结、边板书,填空处尽量由学生填写,随授课进度书写在指定的位置。(分三竖排板书)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






