一、选择题
1.选A [解析] 当x→0时,sinx2~x2,因此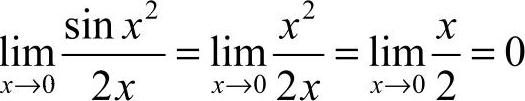 ,故选A.
,故选A.
2.选A [解析] 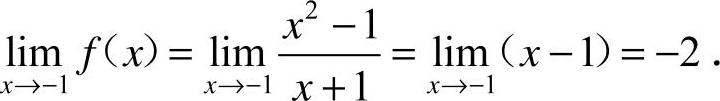
因为f(x)在x=−1处连续,因此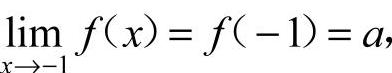 ,a=−2,故选A.
,a=−2,故选A.
3.选D [解析] y=e−2x,y′=(e−2x)′=e−2x(−2x)′=−2e−2x,dy=y′dx=−2e−2xdx,故选D.
4.选A [解析] y=2lnx,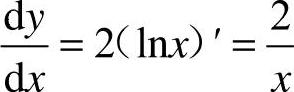 ,
,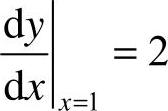 ,故选A.
,故选A.
5.选C [解析] 由不定积分基本公式可知
6.选C [解析] x为f(x)的一个原函数,由原函数定义可知f(x)=x′=1,故选C.
7.选B [解析] 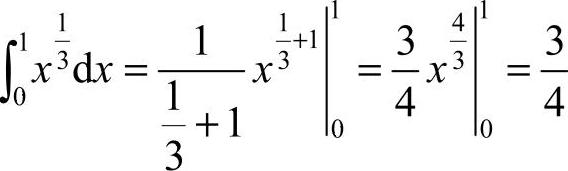 ,故选B.
,故选B.
8.选C [解析] 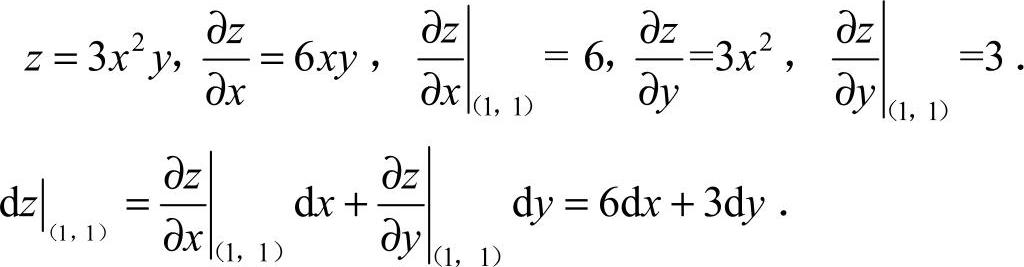 故选C.
故选C.
9.选B [解析] 由二重积分性质可知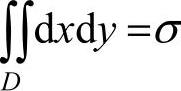 σ,其中σ为积分区域D的面积.此题
σ,其中σ为积分区域D的面积.此题
区域为半径等于1的圆,其面积σ=πr2=π.故选B.
10.选D [解析] 所给方程为可分离变量方程.
分离变量dy=−xdx,
两端分别积分∫dy=−∫xdx,
故选D.
二、填空题
11.e−6 [解析] 由公式 可知,
可知,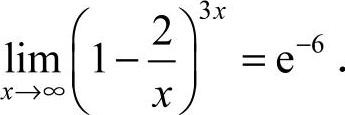
12.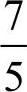 [解析] 所求极限的表达式为分式,分母的极限不为零,因此
[解析] 所求极限的表达式为分式,分母的极限不为零,因此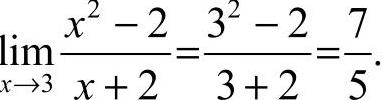
13.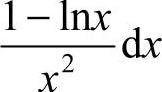 [解析]
[解析] 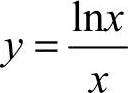 ,
,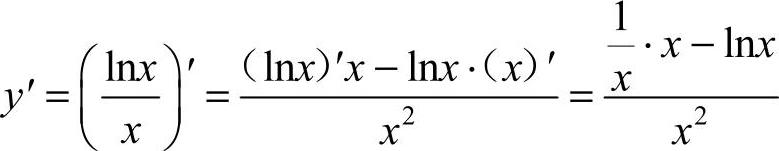
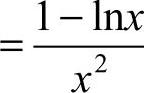 ,
,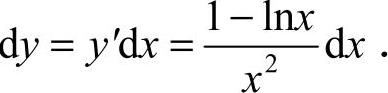
14.3xln23 [解析] y=3x,则y′=3xln3,y′′=(3xln3)′=ln3⋅(3x)′=ln3⋅3xln3=3xln23.
15.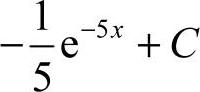 [解析]
[解析] 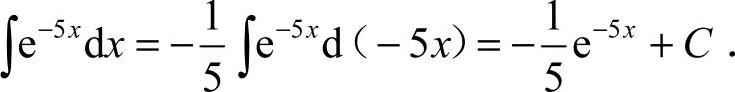
16.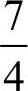 [解析]
[解析] 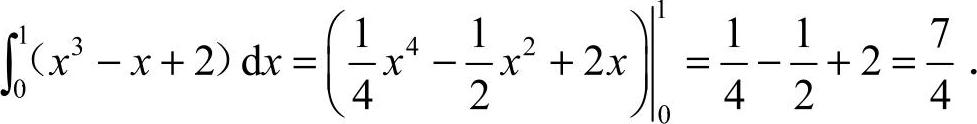 (www.daowen.com)
(www.daowen.com)
17.3x2y [解析] z=x3y+cosy+5,求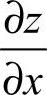 时,认定y为常量,
时,认定y为常量,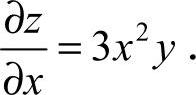
18.x+2y−z−2=0 [解析] 所求平面与已知直线垂直,则平面的法线向量n必定与直线的方向向量s=(1,2,-1)平行.可取n=s=(1,2,-1).又平面过点(1,0,-1).由平面的点法式方程可知所求平面方程为
(x−1)+2(y−0)−[z−(−1)]=0,即x+2y−z−2=0.
19.0 [解析] 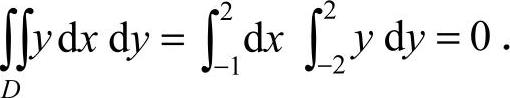
20.1 [解析] 所给幂级数为不缺项情形.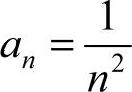 ,
,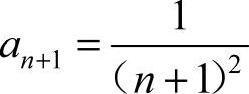 ,
,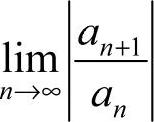
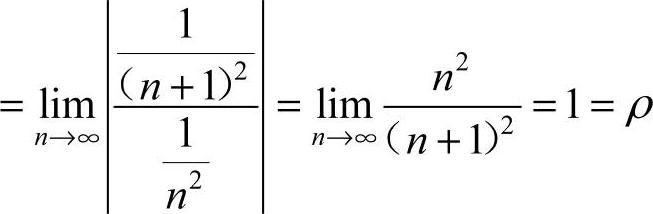 ,则收敛半径
,则收敛半径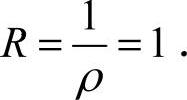
三、解答题
21.解: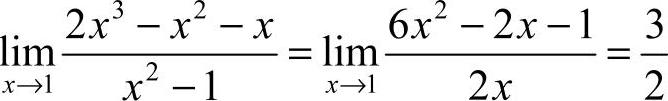 .
.
22.解:y′=(x2)′ex+x2(ex)′=2xex+x2ex=ex(x2+2x).
23.解:∫xsinxdx=x(−cosx)−∫(−cosx)dx=−xcosx+sinx+C.
24.解:y′′−3y′+2y=0,
特征方程 为r2−3r+2=0,
(r−1)(r−2)=0.
特征根为r1=1,r2=2.
方程的通解为y=C1ex+C2e2x.
25.解:z=xsiny,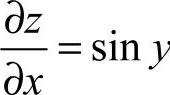 ,
,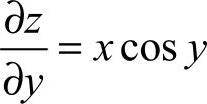 ,
, .
.
26.解:y=x3+2,y′=3x2,y′|x=0=0.
曲线y=x3+2过点(0,2)的切线方程为
y−2=y′|x=0(x−0),即y=2.
D的图形见右图阴影部分.
27.解: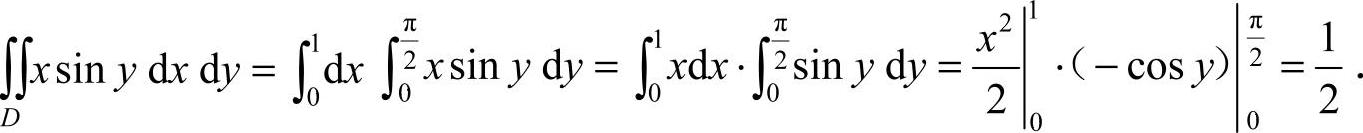
28.解:由于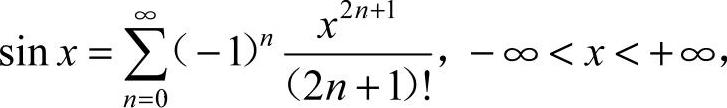
可知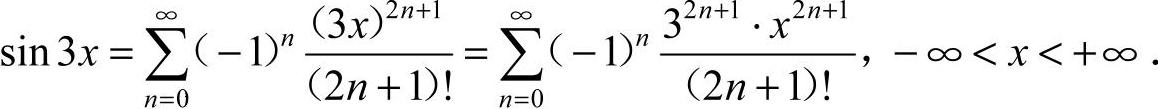
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







