一、选择题
1.选D [解析] 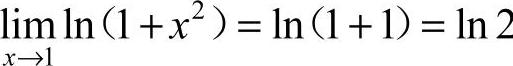 ,因此选D.
,因此选D.
2.选D [解析] y=2−cosx,则y′=2′−(cosx)′=sinx.因此选D.
3.选D [解析] 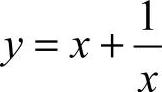 的定义域为(−∞,0),(0,+∞).
的定义域为(−∞,0),(0,+∞).
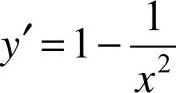 ,
,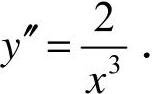
可知当x>0时,y′′>0,曲线为凹;当x<0时,e′′<0,曲线为凸.
因此曲线的凹区间为(0,+∞),应选D.
4.选C [解析]  ,
,
 ,可知y=1为曲线的水平渐近线,因此选C.
,可知y=1为曲线的水平渐近线,因此选C.
5.选D [解析] 
6.选A [解析] 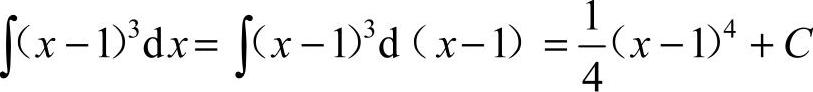 ,因此选A.
,因此选A.
7.选C [解析] 由二次曲面的方程可知应选C.
8.选B [解析] 由级数收敛的定义可知应选B.
9.选A [解析] 积分区域关于y轴对称,被积函数xy为x的奇函数,可知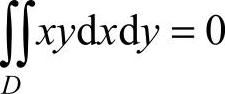 ,应选A.
,应选A.
或者直接计算 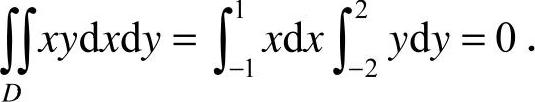
10.选B [解析] z=x2+y2−2x+4y+5,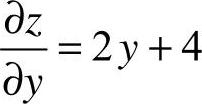 ,故选B.
,故选B.
二、填空题
11.1 [解析] f′(x)=(x−cosx)′=x′−(cosx)′=1+sinx,f′(0)=1.
12.e [解析]  .
.
13.exdx [解析] y′=(ex−2)′=ex,dy=y′dx=exdx.
14. [解析] 因为
[解析] 因为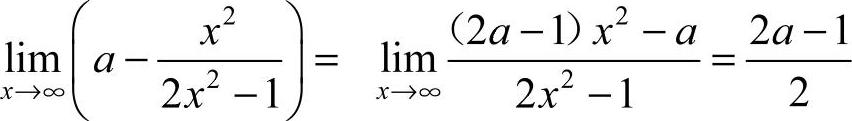 ,由
,由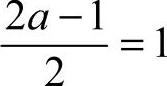 ,得
,得
15.0 [解析] 因为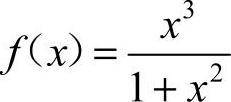 是[-1,1]上的连续奇函数,所以定积分等于0.
是[-1,1]上的连续奇函数,所以定积分等于0.
16.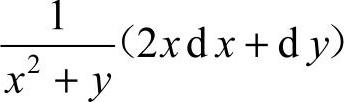 [解析]
[解析] 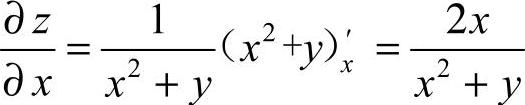 ,
,
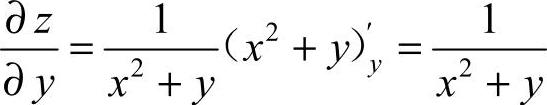 ,所以
,所以 
17.(0,1) [解析]y=1−x−x3,则y′=−1−3x2,y′′=−6x.
令y′′=0得x=0.
当x<0时,y′′>0;x>0时,y′′<0.(www.daowen.com)
当x=0时,y=1.因此曲线的拐点为(0,1).
18. [解析]
[解析] 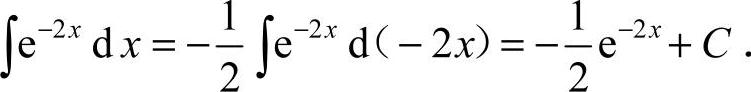
19.(-2,2) [解析] 因为 ,因此
,因此 所以
所以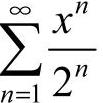 的收敛区间为(-2,2).
的收敛区间为(-2,2).
20.y=2x+C [解析] 分离变量dy=2dx,两端积分∫dy=∫2dx,即y=2x+C.
三、解答题
21.解: 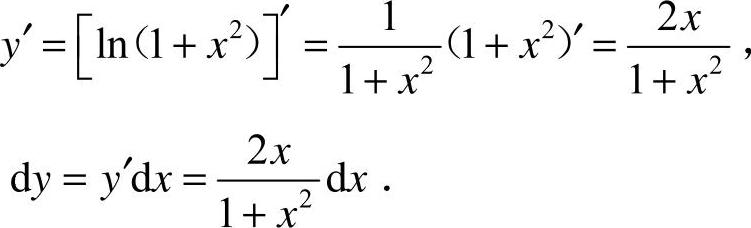
或利用微分公式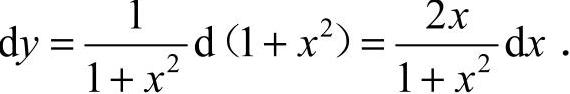
22.解: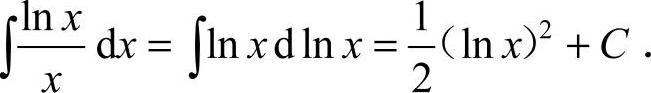
23.解:y=e−3x+x3.
y′=(e−3x)′+(x3)′
=e−3x(−3x)′+3x2
=−3e−3x+3x2.
24.解:令F(x,y,z)=z2+1-xyz
Fx′=−yz,Fy′=−xz,Fz′=2z−xy.
25.解: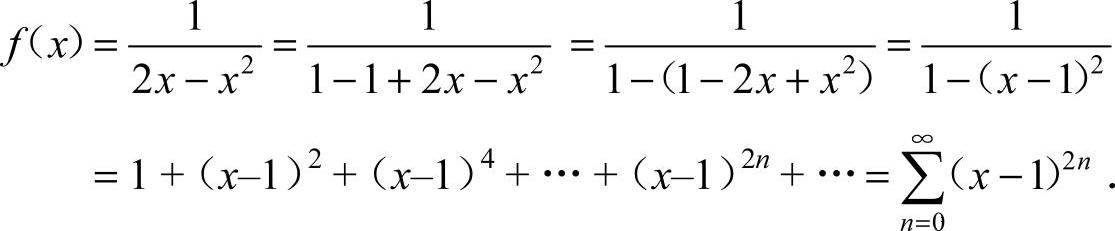
由|(x−1)2|<1,知-1<x-1<1,0<x<2,即收敛区间是(0,2).
26.解: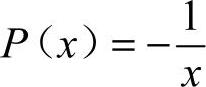 ,Q(x)=lnx.
,Q(x)=lnx.
所以 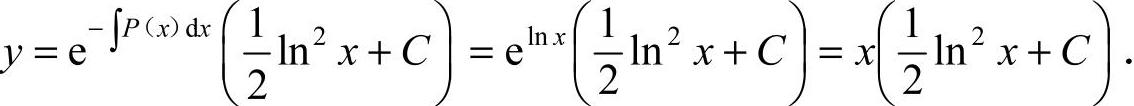
将y|x=1=1代入y式,得 C=1.故所求特解为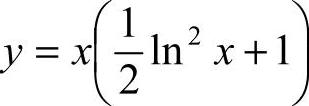 .
.
27.解:所围图形见右图中阴影部分.
28.解: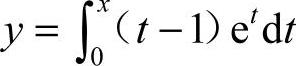 ,
,
则y′=(x−1)ex.
令y′=0,得唯一驻点x=1.
当x<1时,y′<0;x>1时,y′>0.
因此点x=1为y的极小值点.极小值为
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




