一、选择题
1.选D [解析] 由极限的基本公式知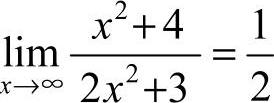 ,因此选D.
,因此选D.
2.选B [解析] 利用公式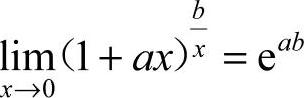 ,
,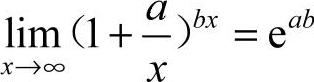 ,可知
,可知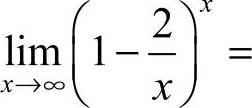
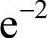 ,因此选B.
,因此选B.
3.选D [解析] 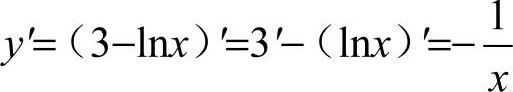 ,因此选D.
,因此选D.
4.选C [解析] y′=[cos(x−3)]′=−sin(x−3)⋅(x−3)′=−sin(x−3),dy=y′dx=−3sin(x−3)dx,因此选C.
5.选C [解析] y=x−ex,y′=1−ex,由y′|x=0=0,可知应选C.
6.选C [解析] 被积函数sin5x为奇函数,积分区间[−1,1]为对称区间.由定积分的对称性质知选C.
7.选A [解析] 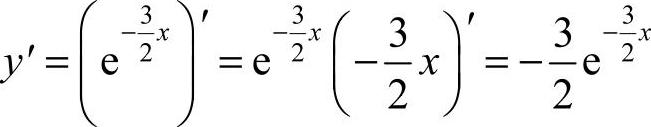 ,因此
,因此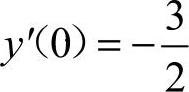 ,可知应选A.
,可知应选A.
8.选B [解析] 由于区域D的图形为由x2+y2=1围成的圆的上半部,所以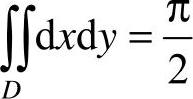 ,故应选B.
,故应选B.
9.选A [解析] 级数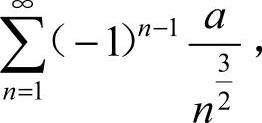
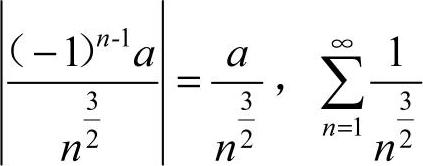 为
为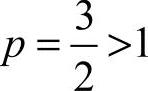 的p级数,因此为收敛级数,由级数性质可知
的p级数,因此为收敛级数,由级数性质可知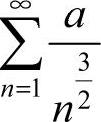 收敛,故
收敛,故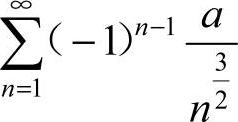 绝对收敛,应选A.
绝对收敛,应选A.
10.选C [解析] 由线性方程解的结构定理知应选C.仅当y1、y2为线性无关特解时,A才正确.
二、填空题
11.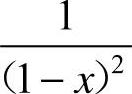 [解析]
[解析] 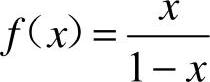 ,
,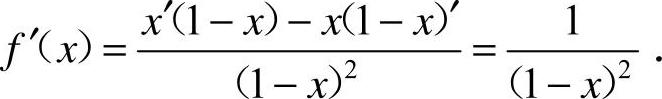
12.−sinxdx [解析] y=cosx,则y′=−sinx,dy=y′dx=−sinxdx.
13.y=1 [解析] 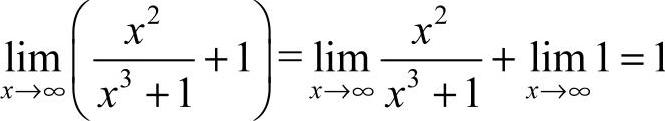 ,
,
故水平渐近线方程是y=1.
14.-2 [解析] 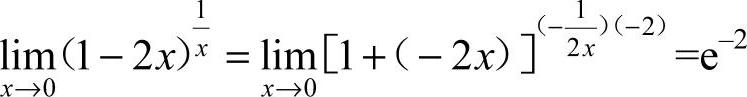 ,由已知,k=-2.
,由已知,k=-2.
15.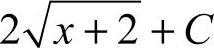 [解析]
[解析] 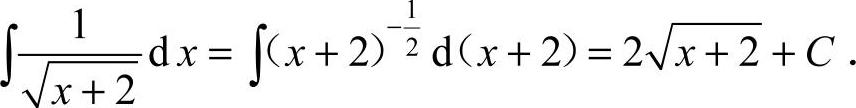
16.-2y [解析] 求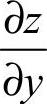 时,将x认定为常量,则
时,将x认定为常量,则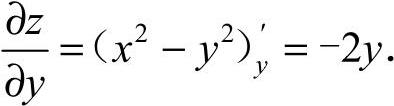
17.(0,2) [解析]y′=3(x2−1),y′′=6x.由y′′=0,有x=0.
当x>0时,y″>0;当x<0时,y′′<0;而x=0时,y=2.故拐点为(0,2).
18.2 [解析] 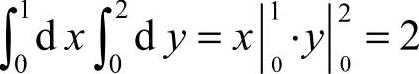 .
.
19.0 [解析] 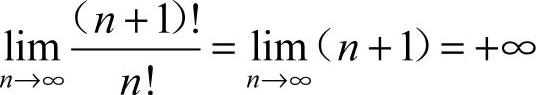 ,所以R=0.
,所以R=0.
20.x2+y2=C [解析] 分离变量,得ydy=xdx.(https://www.daowen.com)
两边积分,有 y2=x2+C.
三、解答题
21.解: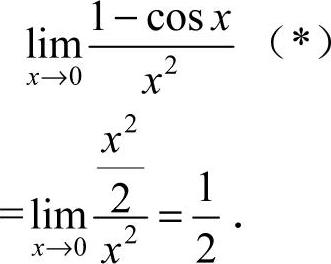
或自()处利用洛必达法则.
22.解: y=x2+2x,
y′=(x2)′+(2x)′=2x+2xln2.
23.解:设F(x,y,z)=ez-z+xy-3=0,
Fx′=y,Fy′=x,Fz′=ez−1,
从而 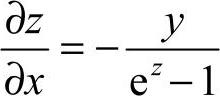 ,
,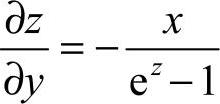 ,
,
故 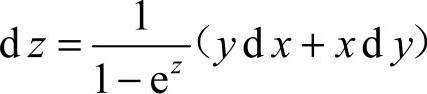 .
.
24.解: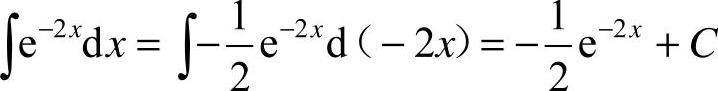 .
.
25.解:y″+4y=0的特征方程为r2+4=0,从而特征根为r1,2=±2i,故其通解为
y1=C1cos2x+C2sin2x.
因为自由项f(x)=e2x,α=2不是特征根.故设y=Ae2x.
代入原方程,有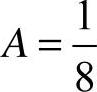 ,
,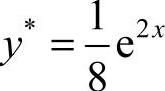 ,
,
故y″+4y=e2x的通解为
26.解:所围图形见右图中阴影部分.
27.解:依题意,面密度函数为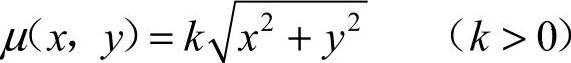 ,
,
所以 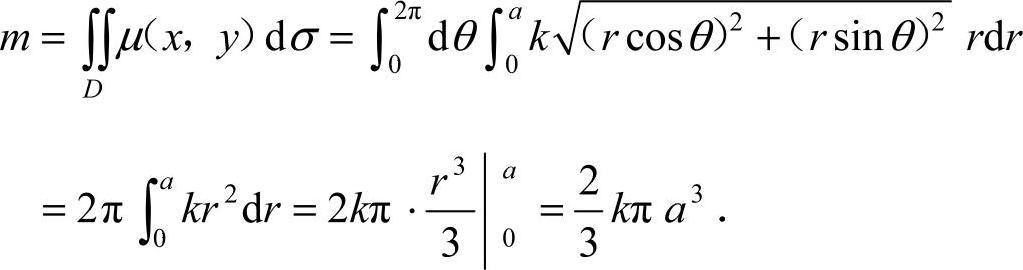
28.解:(1)依题设: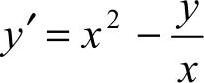 ,即
,即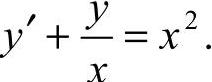
因为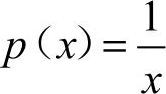 ,q(x)=x2,
,q(x)=x2,
通解为 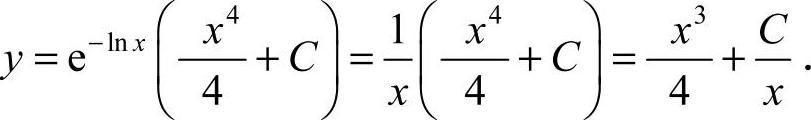
将 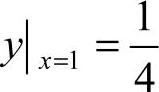 代入通解,得C=0,故所求为
代入通解,得C=0,故所求为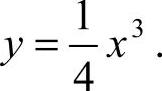
(2)记所求面积为A,则A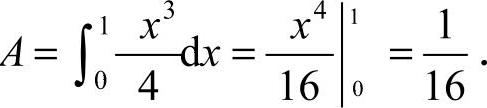
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







