下面以FVaR为例，给出具体算例，其他VaR、CVaR以及FCVaR情形都是类似的方法。

考虑中国金融市场上3种主要资产类型：国债、基金和沪深300股指。

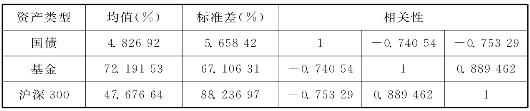
表5-7给出了这3类资产在2005—2010年间的回报率均值、回报率的标准差及资产间的相关系数。

由表5-7可以得出：

表5-7 3类资产的风险—回报数据（2005—2010）

所以，方程组（5-14）可得：

a11x1+a12x2＝b1

根据式（5-13）计算可得：

于是：

x2＝-2．312 183x1+2．211 167

x3＝1．312 183x1-1．211 167

这里取FVaR＝-3．5%，c＝95%，则Φ-1（c）＝1．65，

由式（5-17）得：

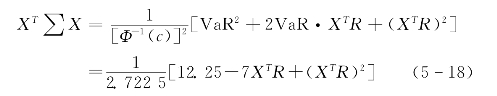
再将R、∑和X＝（x1，x2，x3）T

＝（x1，-2．312 183x1+2．211 167，1．312

183x1-1．211 167）T

代入式（5-18）就得到关于x1的一元二次方程：

即

x2-1．621 295+0．641 397＝0

求出x1的两个根：

x1＝0．936 2或x1＝0．685 1

将x1代入x2和x3中，就得到点A和点B处的投资权重：

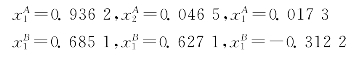
于是，(www.daowen.com)

RA＝8．700 7%，

RB＝33．693 4%

方差为：

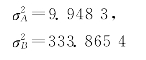
因此，

σA＝3．154 1%

σB＝18．299 3%

故可得出基于VaR约束下投资组合的选择范围是：

8．700 7%≤RP≤33．649 3%，

3．154 1%≤σP≤18．299 3%

这意味着，对于上述范围内任意投资组合，都具有95%的概率使其回报率超过E（rP）-1．65σP，即风险损失超过VaR＝-3．5%的可能性最多只有5%。

在给定上述范围内的投资组合的期望回报率RP（或回报率的标准差σP），可以联立方程（5-16）和方程（5-13）求出最优权重。

例如，给定RA＝20%，则方程（5-13）就具体化为：

4．826 9x+72．191 53x2+47．676 64（1-x1-x2）＝20

进一步化简即为：

42．849 72x-24．514 88x2＝27．676 64

而方程（5-16）为：

225．523 027x1+110．511 591 6x2＝244．359 608 7

联立解方程组得到：

x1＝0．822 7

x2＝0．309 0

因此得出：

x3＝1-x1-x2＝-0．131 7

由式（5-13）或式（5-14），可算得此时投资组合的最小方差为：

故投资组合的标准差为：

σP＝13．555 0%。

同样，若给定投资组合的标准差σP，也可仿照求出得到投资组合的最优权重，进而计算出它们的RP。

综上可以看出，用FVaR以及FCVaR约束的资产组合模型更符合金融市场收益率实际分布模型。这比经典的均值-方差（MV）模型更令人信服，更能解释金融市场的一些实际特征。同时，比起VaR约束的投资组合模型，FVaR或FCVaR约束的投资组合模型，从理论上看起来更完整，更能体现出优越性。实际使用时，根据实际情况选择FVaR和FCVaR中的一种方法即可。