（一）VaR 约束下的均值-方差模型

上述均值-方差模型的优点在于它与机构的VaR测量以及VaR的限额保持了一致性，但存在的问题是：①计算较为复杂；②与目前广为流行的Markowitz 均值-方差模型不一致，增加了投资组合管理者使用时的难度。因此，在已有的均值-方差模型上，增加了VaR约束的投资组合选择问题。下面分别对均值-方差模型同VaR约束条件下的均值-方差模型进行分析。

经典Markowitz均 值-方差模型（Ⅰ）：

其中，R＝（R1，R2，…，Rn）T；Ri＝E（ri）是第i种资产的期望回报率；X＝（x1，x2，…，xn）T是投资组合的权重向量；∑＝（σij）n×n是n种金融资产的协方差矩阵；Rp＝E（rp）和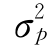分别是投资组合的期望回报率和方差。

考虑VaR约束的投资选择时，给定的置信水平为c，则有VaR定义：

Prob（rp＜-VaR）≤1-c

在模型（Ⅰ）中考虑VaR约束后，经典均值-方差模型可变为模型（Ⅱ）：

在正态分布下，VaR的计算可以表示为：

VaR＝-［E（rp）-Φ-1（c）σp］

其中，Φ（·）是标准正态分布的分布函数。

（二）模型的求解

由于VaR约束的投资组合比较复杂，用传统的Lagrange乘数法无法求解，因此，提出了下面所述的一种几何方法来解决。

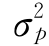假定n种资产组合的权重是x1，x2，…，xn-1，xn，且满足＝1，则投资组合的期望回报率Rp＝E（rp）与方差可分别表示为：

式（5-11）在点（x1，x2，…，xn-1）处的法向量为：(www.daowen.com)

（R1-Rn，R2-Rn，…，Rn-1-Rn）

式（5-12）在点（x1，x2，…，xn-1）处的法向量为：

令

则式（5-12）在点（x1，x2，…，xn-1）处的法向量可简化为：

（P1EQWT，P2EQWT，…，PkEQWT，…，Pn-1EQWT）

由前面给出的临界线定义，可得到如下临界线方程：

由（5-12）式可得到n-2个方程构成的线性方程组：

其中，

基于几何方法的求解，将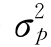转化为如下形式：

根据均值和方差的表达式：

则式5-15可表示为：

因此，VaR约束下的投资组合的选择范围为：