主成分分析（Principal Component Analysis）由Person（1901）提出，是一种通过降维技术把多个变量化为少数几个主成分的方法。这些主成分能够反映原始变量的绝大部分信息，通常表示为原始变量的线性组合。具体如下。

设X1，X2，…，Xp为原有的p个指标，X＝（xij）n×p为其标准化观测矩阵，R＝（rij）n×p为其相关系数矩阵，Li＝（l1i，l2i，…，lpi）T（i＝1，2，…，p）为p个常数向量。

考虑如下线性组合：为p个指标，Yi的样本方差为VaRYi＝RLi，协方差Cov（Yi，Yj）＝LTiRLj（i，j＝1，2，…，p）。希望用较少的新指标代替原来的p个指标，就要求它们含有尽可能多的原指标信息且互不相关。指标信息量的大小通常用该指标的方差来计算，方差越大，信息量就越大，反之则越小。

设R的特征根和对应的正交化单位特征向量分别为λ1≥λ2≥…≥λp≥0和e1，e2，…，eP，则可以证明当Li＝ei时，有VaRYi＝λi，Cov（Yi，Yj）＝0（i，j＝1，2，…，p）。此时令：(www.daowen.com)

则bk和ck分别称为第k个主成分的贡献率和前k个主成分的累积贡献率。累积贡献率表明了前k个主成分占有指标总信息量的份额，一般当ck＝85%时，就可以用k个主成分来表示原有指标而不会损失多少信息。此时得到的综合评价函数为：

在上述步骤中，首先需要对观测矩阵进行标准化处理，使得所有指标在同一个量纲范围内，而且指标存在正指标、负指标和区间指标之分，因此标准化显得非常重要。目前常用的标准化处理的主要方法有Z值法、指数法、线性插值法、百分位法等。这里采用正态标准化处理，即

式中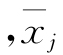为指标j的平均观测值；δj为其标准差。