在金融市场中，一种金融工具波动性越高，其风险就越大。这种波动性或风险性在统计学中是用标准差来度量的，标准差愈大，则对应的风险愈高。然而，下面的例子显示仅仅用标准差来度量金融资产收益率的风险是不够全面的。

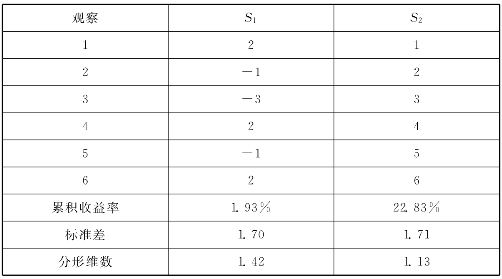
先看如下例子：表3-1中有两个可能的金融收益率序列S1和S2。S1是无趋势序列，而S2是具有明显增强趋势的序列。S1有1．93%的累积收益率，S2累积收益率为22．83%。两者的标准差分别为1．70和1．71，可见用标准差去度量风险是无效的。而用分形维则可以定性地将这两个收益率序列区分开来。时间序列S1的分形维数是1．42，时间序列S2的分形维数是1．13，显然S1是比S2更为参差不齐的序列。

表3-1 分形时间序列

有效市场假说认为，金融资产的价格总是能够完全反映市场上的所有信息。在有效市场假说的框架下，信息在传递过程中没有扭曲，投资者能准确衡量金融资产的基础价值，每一种金融资产的价格完全等同于其基础投资价值。市场上的一切信息都能够反映在金融资产价格中。有效市场假说意味着金融市场中的投机行为从长期来看最终是无利可图的，因为金融资产价格已经完全反映了全部的信息。然而，实际情况并非如此。大多数投资者接到信息后都要等到趋势非常明显后才能作出反应。相反，很多投资者也只是普通的正常人，并不能对每次接受的信息都作出准确快速的反应。特维尔斯基和卡尼曼引领的行为金融学的研究结果表明，投资者并不能在任何情况下，都对信息作出理性无偏的反应。

若从时刻t开始观察一个金融时间序列，观察次数为n，则：(www.daowen.com)

式中，Xt，N为N个期间（可以是周、月、日、年等）的累积离差；eu为该期间内第u次的输入量；MN为N个期间eu的平均量，则：

R＝max（Xt，N）-min（Xt，N）

称之为极差，用原来观察值的标准差S去除极差得到R／S，则R／S称之为重标极差，且：

式中，a为常数，N0为观察次数，H为Hurst指数。