Hurst（1965）在研究尼罗河水坝工程的水库水位时，提出一种全新的统计量——Hurst指数。Hurst是十分有效且强健的统计量，它对于被研究的系统所要的假定条件很少，同时它可以区分随机序列和非随机序列。目前，Hurst指数的估计方法包括绝对值法、R／S分析法、Whittle法、残差方差法、小波分析法等主要方法。

分形分布也称为分形布朗运动（Fractional Brownian Motion，FBM），其数学定义为：

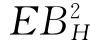令Hurst指数Hε（0，1），对于随机过程｛BH （t），t＞0｝，如果增量ΔBH（τ）＝BH（t+τ）-BH（t）满足服从均值为0、方差为1的高斯分布，则BH（t），t≥0是分形布朗运动。其均值为0，方差为（t）＝t2 H，且具有平稳增量的高斯过程。

协方差为：

它是统计自相似的，即对a＞0｛BH（at），t≥0｝与｛aHBH（t），t≥0｝同分布。H是一个至关重要的参数，称为自相似性参数。增量ΔBH（τ）＝BH（1+τ）-BH（τ）称为分形高斯噪声（Fractional Gaussian Noise）。它是0均值的平稳高斯序列，自协方差函数为：

分形高斯噪声的谱密度为：

式中，k为整数，λ为随机变量。

其中，CH为常数：

分形高斯噪声也是一个自相似过程，即

由于Hurst指数能反映序列的持续性或随机性，在实际中它得到了广泛的应用，在分形分析中起着重要的作用。同时，Mandelbrot（1968）给出了分形布朗运动的自相关函数：(www.daowen.com)

通过传统统计学的推论，如果时间序列是标准的随机游动，那么H＝0．5。当H≠0．5，观测就不是独立的，每个观测都带着在它之前发生的所有时间的“记忆”。

Hurst指数是分形理论研究的重要指标，衡量了时间序列的统计相关性。Hurst指数通常用R／S分析法求得。

Hurst指数取不同值时，时间序列也对应着不同的类型。

（1）当H＝0．5时，时间序列遵循标准的随机游走，此时收益率分布为有效市场假定条件下的正态分布。

（2）当0．5＜H＜1时，时间序列存在着状态持续性，此时时间序列表现为一个趋势增强的序列，收益率分布服从分形布朗运动，而不是有效市场的正态部分。1994年，Peters的研究发现实际生活中大多数的金融时间序列都具备这一特征。H越接近0．5，其噪声越大，趋势越不确定。

（3）当H＜0．5时，时间序列具有逆状态持续性，若序列在上一个期间趋势向上（下），则下一期间就越有可能向下（上）走。H越趋近于零，这种逆持续性就越强。

（4）当H≠0．5时，时间序列存在长期记忆效应。前一期观测值对后一期的观测值会产生长期影响，这种影响用关联尺度函数C来度量：

C＝2（2 H-1）-1

此时分形时间序列是一个有偏的随机游走，将会出现厚尾现象。1972年，Mandelbort证明了H的倒数即为分形分布中的α值（在概率空间的分形维）。