Sklar提出的Copula函数是描述变量之间相关性的一个全新概念。其具体定义为，若F为具有边缘分布为Fi（i=1，2，…，n）的一个联合分布函数，F与各个边缘分布函数之间的关系可以通过一个称之为Copula的函数C进行描述，即：

若边缘分布函数Fi（i=1，2，…，n）的反函数分别是则Copula函数可以通过下式进行求解：

其中ui=Fi （i=1，2，…，n）。如果F是n阶可微的，则其联合密度函数为：

即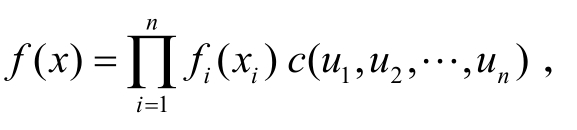则Copula概率密度函数为：(www.daowen.com)

因此，要对Copula函数的参数进行估计，可以对其进行取对数似然函数，然后最优化进行计算，即：

其中ξ=（φ1，…，φn，θ）是包含了边缘分布的参数φi和Copula的参数θ。

如果刻画两个变量之间的相关性，则可以运用二元Copula函数，而常用的二元Copula函数为正态Copula（Norm Copula，N-Copula）和二元t-Copula。Patton依据ARMA（1，10）过程，提出了二元N-copula和二元t-copula的相关系数的方程形式：上式中，函数用来保证方程的结果在区间[-1，1]内，也就说为了描述相关性，相关性介于-1～+1，Φ-1（.）和T-1（；ζ）分别为对应正态分布和t分布累计概率密度函数的逆函数。