对基于分布式滤波的联合定位算法开展实时仿真，其中滤波迭代步长为500 ms，仿真时长为一个轨道周期。

图7-12所示为从飞行器C1和C2在自由漂移过程的定位轨迹。由图可以看到，由于初始条件给定的初始位置存在着一定的偏差，因此初始时刻导航定位轨迹产生一定幅度的振荡。但是，随着滤波迭代时间的增加，导航定位轨迹逐渐收敛至标称轨迹附近。这说明基于分布式滤波的联合定位算法具有较好的稳定性。

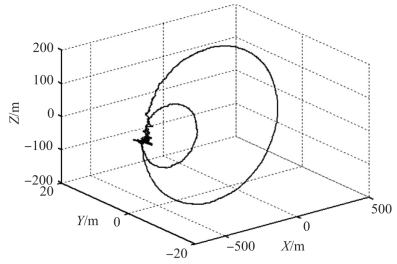
图7-12　从飞行器C1和C2联合定位轨迹

图7-13和图7-14所示为从飞行器自由漂移过程中X和Z向的联合定位误差。由图可以看到，两个从飞行器相对目标航天器各向定位误差在稳态时的精度优于0.5 m。

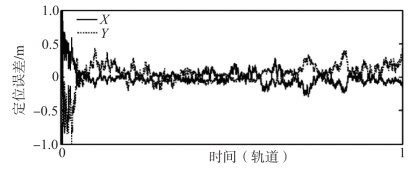
图7-13　从飞行器C1对目标的联合定位误差(www.daowen.com)

此外，在滤波迭代过程中，还可以得到从飞行器C1和C2相对目标航天器的速度分量。图7-15给出了滤波过程中相对速度的估计误差。由图可以看到，相对速度滤波误差优于0.5 cm／s。

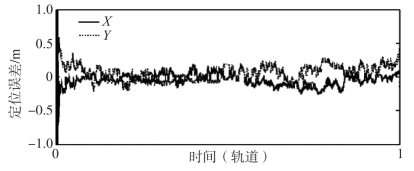
图7-14　从飞行器C2对目标的联合定位误差

图7-15　飞行器对目标的联合定位速度误差

（a）从飞行器C1的速度误差；（b）从飞行器C2的速度误差

通过上述算例仿真可以看到，采用基于分布式滤波的联合定位算法，在从飞行器C1和C2自身不具备对目标航天器测量功能的条件下，通过主飞行器M实现了对目标航天器的精确定位。仿真结果表明，基于分布式滤波的联合定位算法具有精度高、稳定性好的特点，能够较好地满足编队系统对非合作目标航天器的联合定位需求。