滤波迭代过程的稳定性是评价滤波器性能的重要指标，而系统的能观性直接影响滤波精度，因此本部分将采用系统能观性理论，对上述各滤波算法的性能进行分析。定义系统的能观测性矩阵为

式中：A为n×n维常值系统矩阵；H为系统的量测矩阵，则线性系统能观测的充分必要条件为

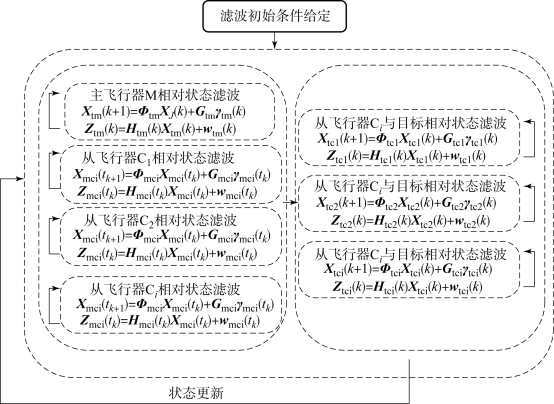
图7-4　分布式定位滤波迭代流程

对于系统的量测矩阵H，有且rank（H）＝r，则线性系统完全能观的充分必要条件为

若P为n×n维可逆矩阵，对线性系统做非奇异变换H′＝HP，A′＝PAP-1，则有

卡尔曼滤波迭代的过程本质上是利用与系统状态相关的量测信息对状态的一步预测进行修正，因此，若线性定常系统是完全能观的，就意味着系统中的全部状态都可以通过量测进行修正，忽略动力学模型不准确等因素，滤波迭代的过程全部状态的估计误差是有界的。相反，如果系统是不完全能观测的，则其中必然有一部分状态分量无法通过量测信息进行修正，因此对应的状态分量的滤波估计误差也是无法收敛的。

线性滤波器包括式（7-36）和式（7-38）所对应的卡尔曼滤波器，对于量测矩阵，有

分别将Hmci、Htci及r代入式（7-46），即可对其能观性矩阵的秩进行计算，限于篇幅原因，上述矩阵计算过程不再赘述，这里只给出结果，即

(www.daowen.com)

显然，上述线性系统是完全能观测的，这说明在分布式定位滤波中的线性部分能够充分利用测量信息对全部系统状态预测值进行修正，因此在理想条件下，滤波误差是有界的。

进一步分析式（7-36）对应的非线性滤波过程的稳定性。非线性量测矩阵是通过局部线性化得到的，这种局部线性化的近似应用对短期非线性系统的可观性还是很有意义的。系统量测矩阵为

结合式（7-8），将非线性量测函数代入式（7-50），可得

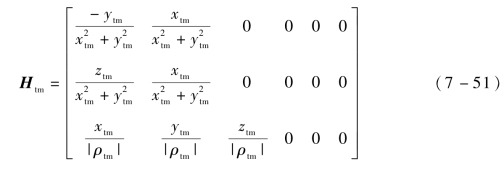
容易证明，在xtm、ytm和ztm全都不为0的情况下，rank（Htm）＝3，此时必然存在可逆矩阵P，有

利用P对近似线性化系统做非奇异变换，有

结合式（7-47），有

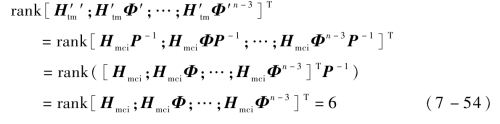
进一步有

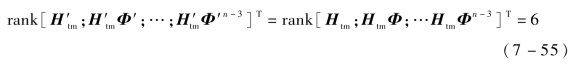
根据能观性理论，说明由式（7-36）和式（7-38）构成的非线性滤波是完全能观的，滤波迭代过程能够充分利用量测信息对其全部状态预测值进行修正。虽然是经过局部线性化得到的，但是上述结论仍然说明在一定时期内滤波是逐渐收敛的。