为了在不显著降低相对导航精度的条件下，减少滤波迭代过程中的计算量，就必须降低系统状态矩阵和量测方程系数矩阵的维数。采用分布滤波方式是实现这一优化目标的有效途径，即在充分考虑主飞行器相对目标航天器以及相对从飞行器的动力学特性的基础上，分别建立关于Xtm（tk）和Xmci（tk）的滤波估计，以最优估计值之和作为从飞行器对目标的测量值，建立从飞行器的量测方程，则

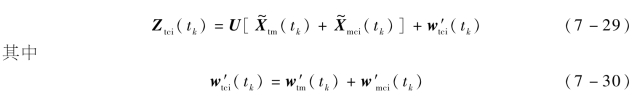
式中：为主飞行器相对目标航天器和从飞行器的滤波误差，结合轨道相对动力学，即可进行卡尔曼滤波。

由于在滤波过程中测量误差已经被有效抑制，因此对比式（7-11）和式（7-30），有(www.daowen.com)

上述滤波算法同时考虑了主、从飞行器和目标航天器三者之间的相对动力学特性，并且采用分布滤波的形式，其滤波迭代算法流程如图7-3所示。由图可以看出，该滤波模型本质上包含三个6维子滤波器，其中第一级迭代滤波，即主飞行器相对目标航天器的滤波、主飞行器和从飞行器相对状态滤波处于并行迭代状态。第一级滤波可有效抑制测量数据的误差，并为第二级滤波提供高精度的量测数据；第二级为从飞行器与目标航天器相对状态的滤波迭代。该滤波算法有效降低了迭代的维数，同时提高了滤波精度。

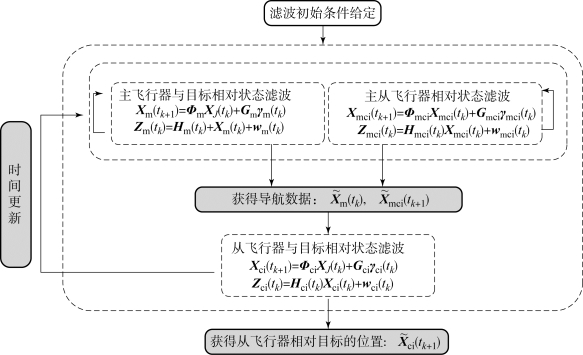
图7-3　分布式滤波迭代流程