假设观测星与非合作目标间的相对位置速度关系及观测方式与3.3节中的算例一致，使用扩维参数自适应卡尔曼滤波算法对表5-2列出了不同的加速度模型进行数值仿真，滤波周期为0.1 s，仿真时长为1 000 s，机动检测器超过阈值时令Pk＝10Pk。仿真结果如图5-12～图5-17所示：图5-14和图5-17分别为机动加速度为常值机动模型以及非常值机动模型时，使用扩维参数自适应卡尔曼滤波算法进行目标跟踪的位置误差和速度误差；图5-12和图5-13分别为机动加速度为常值模型时，机动检测器的值；图5-15和图5-16分别为机动加速度为非常值机动模型时，机动检测器的值。

表5-2　机动加速度模型

表5-2中非常值机动加速度模型的加速度表达式与式（5-35）一致，在未发生机动时，机动加速度为0。

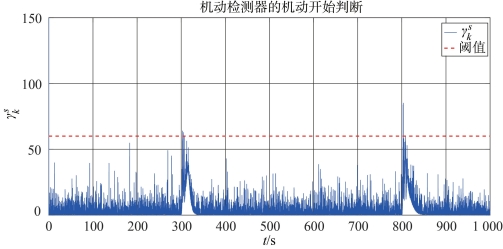
图5-12　机动检测器的值（常值机动）

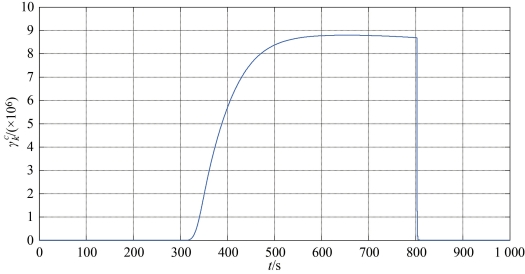
图5-13　机动检测器的值（常值机动）

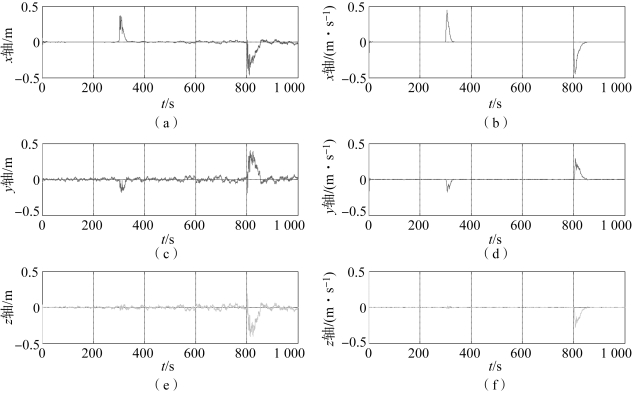
图5-14　扩维参数自适应卡尔曼滤波算法的位置和速度跟踪误差（常值机动）

（a）x轴位置误差；（b）x轴速度误差；（c）y轴位置误差；（d）y轴速度误差；（e）z轴位置误差；（f）z轴速度误差(www.daowen.com)

图5-15　机动检测器的值（非常值机动）

图5-16　机动检测器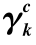的值（非常值机动）

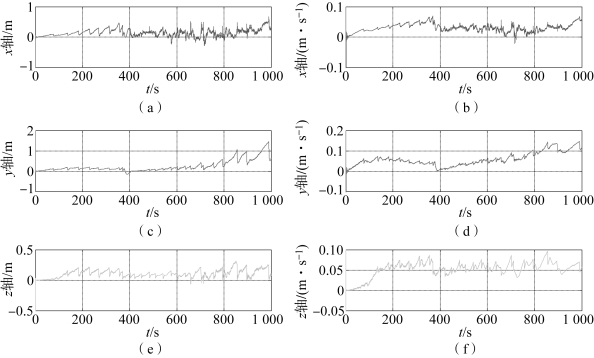
图5-17　扩维参数自适应卡尔曼滤波算法的位置和速度跟踪误差（非常值机动）

（a）x轴位置误差；（b）x轴速度误差；（c）y轴位置误差；（d）y轴速度误差；（e）z轴位置误差；（f）z轴速度误差

由图5-12的机动检测器的值可以看出，的阈值选择为60，在300 s和800 s附近，的值有显著增长，机动检测器判断机动开始的时刻为303.1 s，机动结束的时刻为806.0 s。由图5-13的机动检测器的值可以看出，在800 s后值迅速下降，将阈值选为10 000，则检测到机动结束的时刻为805.9 s，机动检测器判断机动开始和结束的时刻与实际机动开始和结束的时刻大致吻合，但存在一定的滞后。由图5-14中的位置和速度误差曲线可以看出，扩维参数自适应滤波算法在对常值机动目标进行仿真时，总体跟踪精度较好，但在机动开始时刻300 s和机动结束时刻800 s附近时，位置和速度误差明显增大。结合机动检测器的仿真可知，误差增大的原因是机动加速度变化率发生突变和机动检测器不可避免的时间滞后，导致在机动发生时协方差矩阵没有及时增大，使得机动发生时仍使用传统的扩维卡尔曼滤波算法对目标进行跟踪，导致误差短时间内迅速增大。同理，当目标机动结束时，由于机动加速度变化率突变和时间滞后两种因素，导致在机动结束时刻也会出现误差增大的情况。

由图5-15的机动检测器的值可以看出，当目标发生连续的非常值加速度机动时，的值经常超过阈值。这是由于扩维卡尔曼滤波算法本身对时变机动加速度的估计效果较差，增大误差协方差矩阵只能在短时间内一定程度上改善模型不匹配造成的误差发散情况，因此当非常值机动加速度持续一段时间，会导致再次超过阈值。此时，为了防止滤波算法发散，使得估计均方误差继续增大。与此同时，由图5-16可以看出，会迅速降低，会判断机动已经结束，这显然与实际不符。当系统判断机动结束后，算法回到误差协方差矩阵参数不变的扩维卡尔曼滤波算法，但此时目标仍在进行非常值机动，由于扩维卡尔曼滤波算法在非常值机动模型下跟踪精度较差，因此测量残差会增大，值随之增大，从而使得在非合作目标进行非常值机动的过程中，判断机动开始的值会反复超过阈值，判断机动开始的值不能真实地反映机动终止的时刻。由图5-17中的位置和速度误差曲线可以看出，扩维参数自适应滤波算法在对非常值机动目标进行仿真时，误差曲线仍有发散的趋势，这是由于扩维卡尔曼滤波算法本身对具有时变机动加速度的目标跟踪效果较差所导致的，且随着时间的增长，误差曲线所含的噪声越大，这是由于增大误差协方差矩阵所导致的，原理与衰减记忆滤波法类似。因此，扩维参数自适应滤波算法对非常值机动模型跟踪效果较好，但会随着时间的增长，精度越来越低。

综上所述，扩维参数自适应滤波不需要对目标的机动特性作任何的先验假设，对无机动和发生常值机动的非合作目标有较好的跟踪效果，但是对于非常值机动加速度模型跟踪效果会随着时间的增长逐渐变差。另外，该方法严重依赖于机动检测，但是机动发生与检测到机动发生之间必然存在着时间滞后，滞后时间的长短取决于阈值的选择。阈值过小，会导致算法不断增大协方差矩阵值，使得引入的噪声过多，导致精度过低；阈值过大，则不能检测到机动的发生，并且无论阈值选择合适与否均存在着不可避免的误差。