假设观测星和非合作目标均运行在高为700 km的圆轨道上，并且两者之间的距离远小于轨道半径，初始相对位置向量为r＝［500 m，300 m，200 m］T，相对速度向量为v＝［10 m／s，10 m／s，5 m／s］T，滤波采样周期为0.1 s，总时长为1 000 s，初始位置和速度偏差为xerror＝［300 m，200 m，100 m，10 m／s，15 m／s，20 m／s］T。选取C-W方程作为系统的动力学模型，将位置和速度作为系统的状态变量x＝［x，y，z，］T，控制驱动矩阵和过程噪声驱动矩阵分别为Bk＝［03×3　I3×3］T和Gk＝I6×6。观测星采取可见光相机与激光测距仪的组合测量方式，获得测角和测距信息。其中，相机测量精度为1″，激光测距仪测距精度为0.1 m（3σ）。

非合作机动目标的机动加速度模型可分为三类：第一类是目标不发生未知机动，即机动加速度为0，称为无机动模型；第二类是目标的机动加速度为常值，即机动加速度变化率为0，称为常值机动模型；第三类是目标的机动加速度为时变量，即机动加速度变化率不为0，称为非常值机动模型。表5-1给出了本算例的三种机动加速度模型的具体值。

表5-1　机动加速度模型

表5-1中非常值机动模型中uVA的表达式为

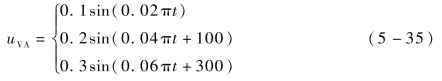
下面分别采用扩展卡尔曼滤波算法、衰减记忆滤波算法以及扩维卡尔曼滤波算法对表5-1中三种具有不同机动加速度的系统进行数值仿真，仿真结果如图5-1～图5-10所示。

1.无机动模型仿真对比

当机动加速度模型为无机动模型时，即非合作目标未发生机动时，使用扩展卡尔曼滤波算法、衰减记忆滤波算法（α＝1.05）以及扩维卡尔曼滤波算法进行目标跟踪时的位置误差和速度误差分别如图5-1～图5-3所示。

由图5-1～图5-3可以看出，扩展卡尔曼滤波算法在目标未发生机动时的位置估计误差不大于0.015 m，速度估计误差不大于5×10-5 m／s；衰减记忆滤波算法在目标未发生机动时的位置估计误差不大于0.3 m，速度估计误差不大于0.05 m／s，并且有逐渐发散的趋势；扩维卡尔曼滤波算法的位置误差不大于0.04 m，速度误差不大于0.002 m／s。综上所述，当非合作目标不发生机动时，这三种滤波算法在目标跟踪时的跟踪精度最高的是扩展卡尔曼滤波算法，其次是扩维卡尔曼滤波算法，最低的是衰减记忆滤波算法。

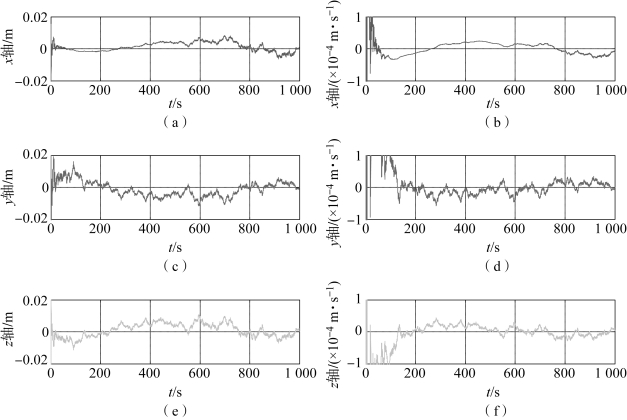
图5-1　扩展卡尔曼滤波算法的位置和速度跟踪误差（无机动）

（a）x轴位置误差；（b）x轴速度误差；（c）y轴位置误差；（d）y轴速度误差；（e）z轴位置误差；（f）z轴速度误差

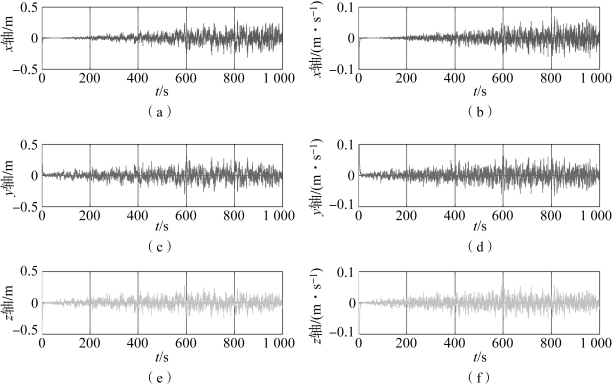
图5-2　衰减记忆滤波算法的位置和速度跟踪误差（无机动，α＝1.05°）

（a）x轴位置误差；（b）x轴速度误差；（c）y轴位置误差；（d）y轴速度误差；（e）z轴位置误差；（f）z轴速度误差

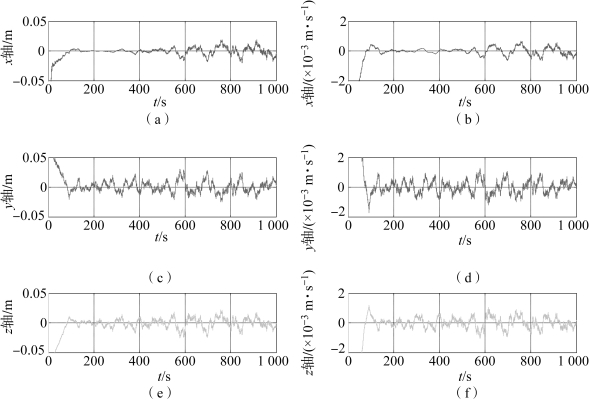
图5-3　扩维卡尔曼滤波算法的位置和速度跟踪误差（无机动）

（a）x轴位置误差；（b）x轴速度误差；（c）y轴位置误差；（d）y轴速度误差；（e）z轴位置误差；（f）z轴速度误差

当目标不发生机动时，由于系统的动力学模型与实际运动状态相符，此时扩展卡尔曼滤波算法为最优估计，因此估计误差最小，跟踪精度最高。扩维卡尔曼滤波算法与扩展卡尔曼滤波算法相比精度略低，这是由于算法将系统中的噪声信息当作机动加速度信息进行了估计，即实际机动加速度为0时，估计的机动加速度不为0。但是却将估计的伪加速度值作为系统动力学补偿量，所以导致扩维卡尔曼滤波算法的精度较扩展卡尔曼滤波算法低。衰减记忆滤波算法与扩展卡尔曼滤波算法相比精度变低是由于衰减记忆因子的引入，因为记忆因子的增大会使在估计中量测数据的使用权重增大，引入了比扩展卡尔曼滤波算法更多的量测噪声，并且会随时间积累。因此，会出现图5-2中相对位置和速度误差开始较小，随着时间的增长，误差逐渐增大的现象。

2.常值机动模型仿真对比

当机动加速度模型为常值机动模型时，即非合作目标的机动加速度为常值时，使用扩展卡尔曼滤波算法、衰减记忆滤波算法（α＝1.05，α＝1.08）以及扩维卡尔曼滤波算法进行目标跟踪时的位置误差和速度误差分别如图5-4～图5-7所示。

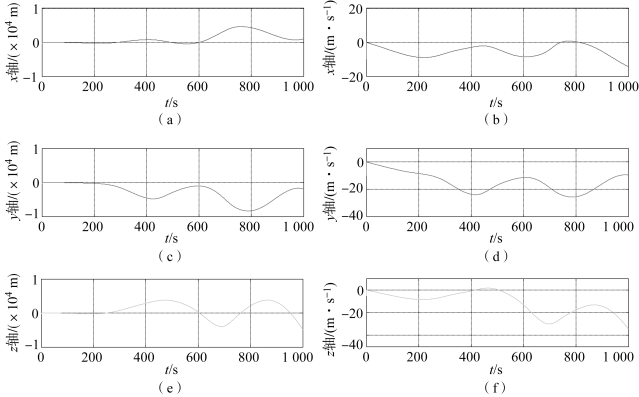
图5-4　扩展卡尔曼滤波算法的位置和速度跟踪误差（常值机动）

（a）x轴位置误差；（b）x轴速度误差；（c）y轴位置误差；（d）y轴速度误差；（e）z轴位置误差；（f）z轴速度误差

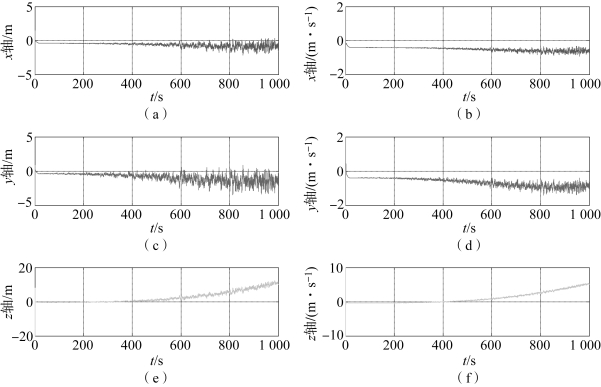
图5-5　衰减记忆滤波算法的位置和速度跟踪误差（常值机动，α＝1.05）(www.daowen.com)

（a）x轴位置误差；（b）x轴速度误差；（c）y轴位置误差；（d）y轴速度误差；（e）z轴位置误差；（f）z轴速度误差

图5-6　衰减记忆滤波算法的位置和速度跟踪误差（常值机动，α＝1.08）

（a）x轴位置误差；（b）x轴速度误差；（c）y轴位置误差；（d）y轴速度误差；（e）z轴位置误差；（f）z轴速度误差

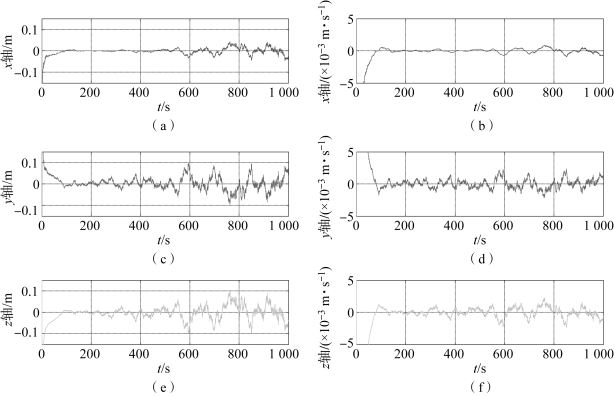
图5-7　扩维卡尔曼滤波算法的位置和速度跟踪误差（常值机动）

（a）x轴位置误差；（b）x轴速度误差；（c）y轴位置误差；（d）y轴速度误差；（e）z轴位置误差；（f）z轴速度误差

由图5-4～图5-7可以看出，扩展卡尔曼滤波算法在目标机动加速度为常值时的位置估计误差峰值接近104 m，速度估计误差峰值接近40 m／s，且呈现严重的发散趋势；当衰减记忆因子α＝1.05时，衰减记忆滤波算法在目标机动加速度为常值时的位置估计误差不大于20 m，速度估计误差不大于10 m／s，并且有逐渐发散的趋势；扩维卡尔曼滤波算法的位置误差不大于0.1 m，速度误差不大于0.004 m。

综上所述，当非合作目标的机动加速度为常值时，这三种滤波算法中仅有扩维卡尔曼滤波算法能保持较高的跟踪精度，其次为衰减记忆滤波算法，扩展卡尔曼滤波算法已完全失去跟踪的功能。

当非合作目标发生常值机动时，扩展卡尔曼滤波算法出现误差发散导致目标丢失的原因是建立的系统动力学模型中不包含机动加速度项，即动力学模型与实际运动状态不匹配，此时扩展卡尔曼滤波算法已不是最优估计。故当系统动力学模型无法准确获得或受到外界干扰时，扩展卡尔曼滤波算法不适用于状态估计，即扩展卡尔曼滤波算法不适用于发生机动的目标跟踪。

与扩展卡尔曼滤波算法的发散比较，衰减记忆滤波算法的跟踪精度有显著提高，这是因为衰减记忆因子的引入增加了量测数据在状态估计时的权重，在一定程度上能够缓解模型误差带来的滤波发散问题，改善了扩展卡尔曼滤波算法，有较强的抗干扰能力。由图5-5和图5-6可以看出，衰减记忆因子越大，衰减记忆滤波算法的估计误差变小，即抗干扰性变强。但是误差估计曲线所含的噪声项也随之增大，因此不可盲目增大衰减记忆因子以达到抑制滤波发散的目的。衰减记忆滤波算法误差曲线中的噪声也随时间的积累而持续增大，这也是衰减记忆滤波的一个主要缺点，因此该算法仅能适用于低精度的目标跟踪。

当非合作目标发生常值机动时，扩维卡尔曼滤波算法能保持较高精度的原因是扩维后的状态变量中加速度项可以实现对机动加速度的实时估计。虽然加速度估计项中可能含有由于噪声引起的伪加速度值，但是由于噪声引起的伪加速度值远远小于机动加速度值，因此对状态估计的影响较小，故扩维卡尔曼滤波算法能在非合作机动目标发生常值机动时实现高精度的跟踪。

3.非常值机动模型仿真对比

当机动加速度模型为非常值机动模型时，即非合作目标的机动加速度时变时，使用扩展卡尔曼滤波算法、衰减记忆滤波算法（α＝1.05）及扩维卡尔曼滤波算法进行仿真验证，两种算法在目标跟踪时的位置误差和速度误差分别如图5-8～图5-10所示。

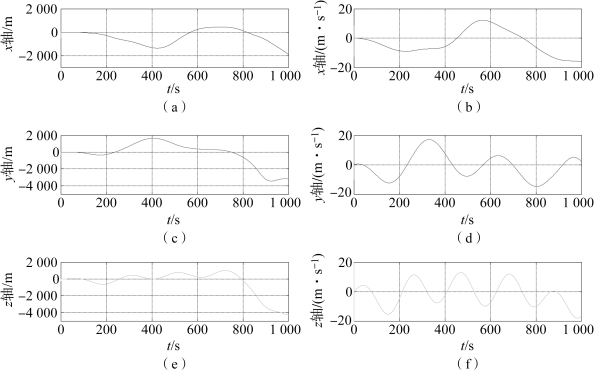
图5-8　扩展卡尔曼滤波算法的位置和速度跟踪误差（非常值机动）

（a）x轴位置误差；（b）x轴速度误差；（c）y轴位置误差；（d）y轴速度误差；（e）z轴位置误差；（f）z轴速度误差

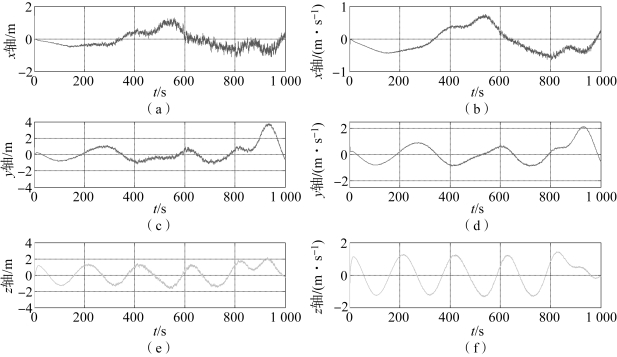
图5-9　衰减记忆滤波算法的位置和速度跟踪误差（非常值机动，α＝1.05）

（a）x轴位置误差；（b）x轴速度误差；（c）y轴位置误差；（d）y轴速度误差；（e）z轴位置误差；（f）z轴速度误差

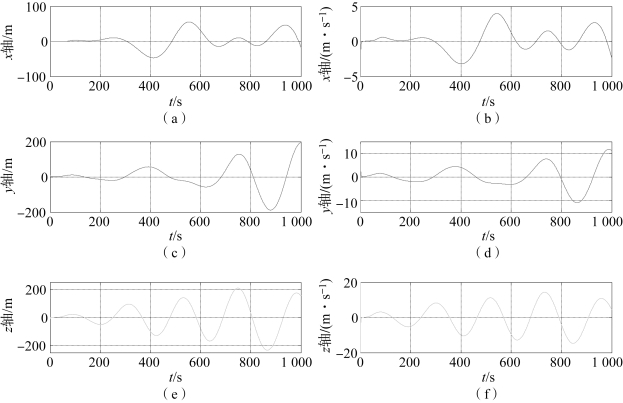
图5-10　扩维卡尔曼滤波算法的位置和速度跟踪误差（非常值机动）

（a）x轴位置误差；（b）x轴速度误差；（c）y轴位置误差；（d）y轴速度误差；（e）z轴位置误差；（f）z轴速度误差

由图5-8～图5-10可以看出，扩展卡尔曼滤波算法在目标机动加速度为常值时的位置估计误差峰值接近4 000 m，速度估计误差峰值接近20 m／s，与常值机动模型一样呈现严重的发散趋势；衰减记忆滤波算法在目标机动加速度为常值时的位置估计误差不大于4 m，速度估计误差不大于2 m／s，误差曲线有发散趋势；扩维卡尔曼滤波算法的位置误差峰值接近200 m，速度误差峰值接近20 m，误差曲线严重发散。综上所述，当非合作目标的机动加速度时变时，这三种滤波算法的目标跟踪效果均不理想，其中衰减记忆滤波算法跟踪精度相对较好，其次为扩维卡尔曼滤波算法，最差的为扩展卡尔曼滤波算法。

扩展卡尔曼滤波算法误差曲线发散的原因与目标发生常值机动一样，是由于未知机动使得建立的动力学模型与实际运动不符。与常值机动模型相比，扩维卡尔曼滤波算法的跟踪精度大大降低。由图5-10可见，估计误差曲线严重发散，并且与机动加速度的变化率有一定的关系。这是由滤波算法的初始假设导致的，由于没有目标机动特性的先验信息，因此假设机动加速度的变化率为0，导致算法对加速度时变的机动目标跟踪效果较差。由图5-10可见，z轴误差最大，加速度变化率越大，跟踪精度越低。衰减记忆滤波算法由于衰减记忆因子的引入，增大了量测数据在状态估计中的权重，改善了扩展卡尔曼滤波算法对具有时变机动加速度模型的非合作目标的跟踪效果，与其他两种算法相比有较强的抗干扰性。

综上所述，扩展卡尔曼滤波算法在非合作目标不发生机动时，跟踪精度最高，但是不适用于机动目标跟踪。衰减记忆滤波算法在非合作目标不发生机动时，跟踪精度较低，但抗干扰性较好，适合对短时间及低精度的机动目标进行粗跟踪。扩维卡尔曼滤波算法在非合作目标的机动加速度为常值时，跟踪效果非常好；当目标不发生机动时，跟踪精度较好，略低于扩展卡尔曼滤波算法，但是不适用于对具有时变机动加速度的机动目标进行跟踪。