在4.5.1节中，介绍了根据目标边缘计算与之具有等价二阶中心矩椭圆的特征。考虑到目标成像面积较小，若仅依据目标边缘进行二阶中心矩的计算，可能会在相邻帧的图像中导致二阶中心矩的抖动。因此，考虑用整个轨迹计算与轨迹具有等价二阶中心矩的椭圆域。首先，对目标成像轨迹进行连通域检测，并编号。

如图4-14所示，图（a）为原始图像，图（b）为满足灰度阈值的像素点，图（c）为连通域检测后的标记结果。八连通域检测方法是指遍历灰度矩阵A中像素点A（i，j）周围的8个像素点A（i-1，j-1）、A（i-1，j）、A（i-1，j＋1）、A（i，j-1）、A（i，j＋1）、A（i＋1，j-1）、A（i＋1，j）、A（i＋1，j＋1），若周围的8个像素点中存在满足灰度阈值的像素点，则认为该像素点与A（i，j）连通。遍历图像中每个像素，进行八连通域检测，并对每个连通区域进行编号。

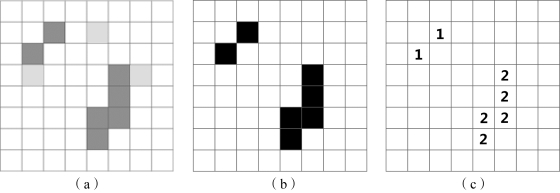
图4-14　八连通域检测示意图

（a）原始图像；（b）满足灰度阈值像素点；（c）连通域检测后标记结果

根据式（4-25），分别令p＝2，q＝0，p＝0，q＝2，p＝1，q＝1，得椭圆在O′-u′v′坐标系下的二阶原点矩为(www.daowen.com)

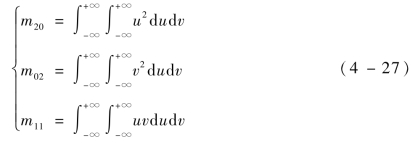
因此，椭圆在O-uv坐标系下的二阶中心矩μ20＝m20，μ02＝m02，μ11＝m11。为了便于描述椭圆域的二阶中心矩与椭圆长半轴、短半轴及长轴与横轴夹角的关系，令u＝r·cosα，v＝r·sinα，在椭圆域内积分，式（4-27）可以变换为

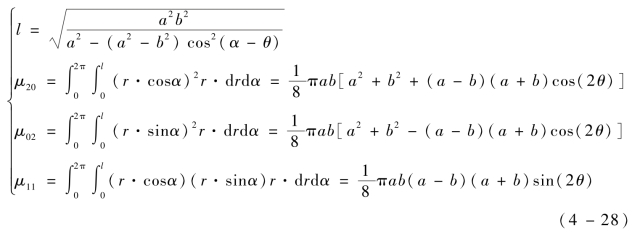
由式（4-28）可得

至此，可以根据目标成像轨迹计算得到具有等价二阶中心矩的椭圆的成像面积m00、形心（u0，v0）、椭圆长半轴a、椭圆短半轴b、椭圆离心率e、椭圆长轴与横轴正向夹角θ。这些参数可用于指定帧间匹配准则，从而计算出目标的位置。