当空间目标相对于航天器相对运动角速度较大时，目标成像轨迹近似于一条直线。因此，对拖尾目标的检测转变为在图像中检测直线的问题。解决直线检测问题的一种方法是在图像中移动一个合适形状和大小的掩膜，寻找图像与掩膜间的相关性。然而，由于形状变形、旋转、缩放等原因，掩膜常常与待处理的数据中物体的表示相差太大。

另一种非常有效的解决该问题的方法是Hough变换。Hough变换于1962年由Paul Hough提出，其基本思想是运用参数空间进行坐标转换，并且通过累计投票的方法得到最终检测结果。最初的Hough变换是设计用来检测直线和曲线的。

下面以直线检测为例，说明Hough变换方法的基本思想。二维平面上的一条直线可以用两点A＝（xa，ya），B＝（xb，yb）定义，如图4-10（a）所示。过点A的所有直线可由ya＝k1xa＋b1表示，这意味着同一个方程可以解释为参数空间（k1，b1）的方程，过点A的所有直线可以表示为方程ba＝-xaka＋ya，如图4-10（b）所示。同理，过点B的直线可以表示为bb＝-xbkb＋yb。在参数空间（k，b）中，两条直线唯一的公共点是在原图像空间中表示连接点A和B的唯一存在的直线。

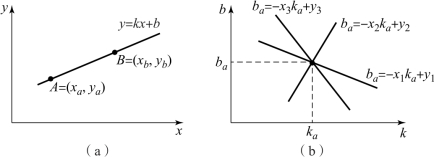
图4-10　Hough变换直线检测

这意味着图像中的每条直线在参数空间（k，b）中由单独一个点表示，直线的任何一部分都变换为同一个点。直线检测的主要思想是确定图像中所有的直线像素，将通过这些像素的所有直线变换到参数空间的对应点，在参数空间检测点（k，b），该点是由图像中频繁出现的直线y＝kx＋b的Hough变换的结果。

考虑到直线存在斜率无穷大的情况，因此常采用极坐标表示直线，但是其转换原理与上述方式基本相同。在Hough变换中，直线的极坐标表示形式为

(www.daowen.com)

此时，直线参数空间变为（ρ，θ），ρ为直线到原点的距离，θ决定直线的斜率。

定义二维参数空间H（ρ，θ），用如下表达式将ρ、θ离散化：

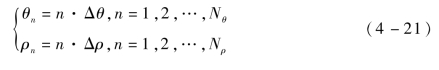
式中：Nθ为参数θ的分割段数，Δθ＝π／Nθ；Nρ为参数ρ的分割段数；L为图像中距原点距离的最大值，Δρ＝L／Nρ。

基于此，对模拟的目标拖尾轨迹进行Hough变换直线检测，其检测结果如图4-11所示。

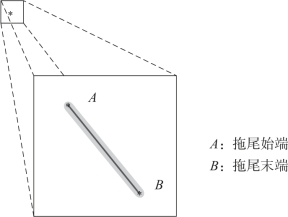
图4-11　Hough变换检测目标拖尾轨迹