【摘要】:空间相机通过成像透镜将空间目标投影到摄像机二维像平面上,投影过程可用成像变换描述,即相机成像模型。首先定义如下坐标系:图4-1相机针孔成像模型①数字图像坐标系o-uv。相机坐标系下三维空间上的点P线性映射到图像物理坐标系下的p′点。
空间相机通过成像透镜将空间目标投影到摄像机二维像平面上,投影过程可用成像变换描述,即相机成像模型。采用针孔成像模型描述映射关系,相机针孔成像模型如图4-1所示。首先定义如下坐标系:
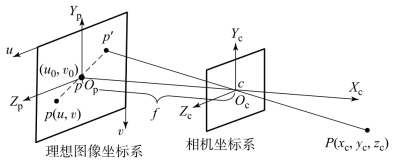
图4-1 相机针孔成像模型
①数字图像坐标系o-uv。数字图像坐标系以图像左上角为原点,描述像素位于数字图像的列数和行数。
②图像物理坐标系O-XpYpZp。图像物理坐标系原点位于成像平面中心,Xp轴垂直于成像平面指向镜头方向,Yp轴与数字图像坐标系v轴反向,Zp与Xp、Yp构成右手笛卡儿坐标系。
③相机坐标系Oc-XcYcZc。坐标系原点Oc为相机光心,Yc、Zc分别与成像平面坐标系中的Y、Z轴平行,Xc为摄像机的光轴,与图像平面垂直。
④世界坐标系Ow-XwYwZw。为了便于分析,此处取世界坐标系与相机坐标系重合。(https://www.daowen.com)
在图4-1中,f为相机焦距。相机坐标系下三维空间上的点P(xc,yc,zc)线性映射到图像物理坐标系下的p′点。根据透镜成像原理,P点在图像坐标系对应的点p′为倒立相反的,需要经过180°旋转,才能得到人眼看到的图像。经过180°旋转后,得到p。在模拟目标图像时,假设相机不存在畸变。由比例关系,可得相机坐标系下目标位置P(xc,yc,zc)与理想图像坐标系下成像点p(yp,zp)的对应关系为
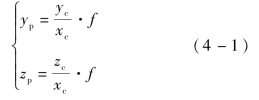
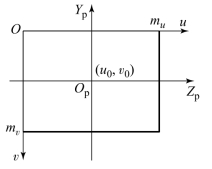
图4-2 数字图像坐标系
记电荷耦合器体(CCD)面阵为mu×mv像素,每个像素点物理几何尺寸为dY×dZ,取数字图像坐标系为CCD面阵中点,结合图4-2与式(4-1),可得
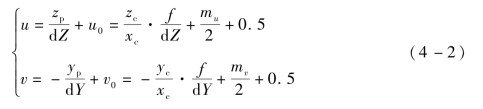
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章






