闪烁噪声广泛地存在于雷达测量中。在复杂目标进行运动时，各个部位产生的回波在幅值和相位上发生起伏，引起回波波前畸变，由此产生的一类噪声称为闪烁噪声。闪烁噪声具有厚尾特性，其导致的问题在于量测野值的频繁出现。在建模时，可将闪烁噪声视为小方差高斯分布和大方差高斯分布的叠加，即

式中：f（vk）为闪烁噪声的概率密度；fg（vk）为小方差高斯分布的概率密度；ft（vk）为大方差高斯分布的概率密度；ε为闪烁的强度。

若式（3-70）等号右侧的两个高斯分布均值为0，则闪烁噪声的方差var（vk）可计算如下：

式中：varg（vk）和vart（vk）分别为两个高斯分布的方差。

假设fg（vk）和ft（vk）的均值为0，方差分别为1和50，ε＝0.2，与f（vk）等均值、等方差的高斯分布记为f′（vk）。根据f（vk）和f′（vk）产生两组随机数，如图3-18所示，由图中可以明显观察到闪烁噪声的野值。

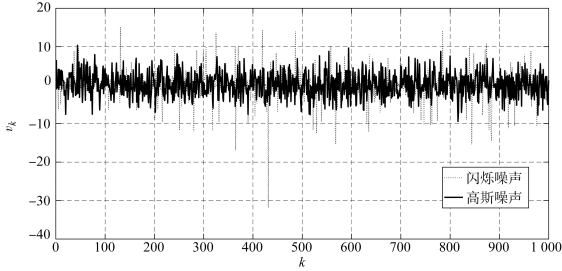
图3-18　闪烁噪声和高斯噪声

UKF属于高斯滤波器，在处理闪烁噪声时必然会产生较大的误差。量测野值会使似然函数落在转移密度的尾部，BPF和GPF由于利用转移密度生成重要性密度，未考虑当前量测值。因此，在理论上会对量测野值敏感，发生权值退化，该问题同样可由图3-12来说明。AVPF和UGPF结合当前量测值生成重要性密度，有望优化粒子分布，克服BPF和GPF对量测野值敏感的缺陷。假设相对测量雷达的闪烁噪声服从如下厚尾分布：

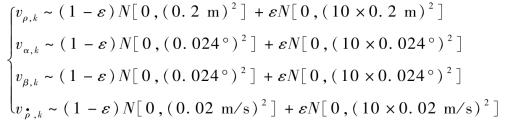
式中：ε＝0.2。取粒子数N＝3 000，蒙特卡罗仿真实验次数NMC＝20。

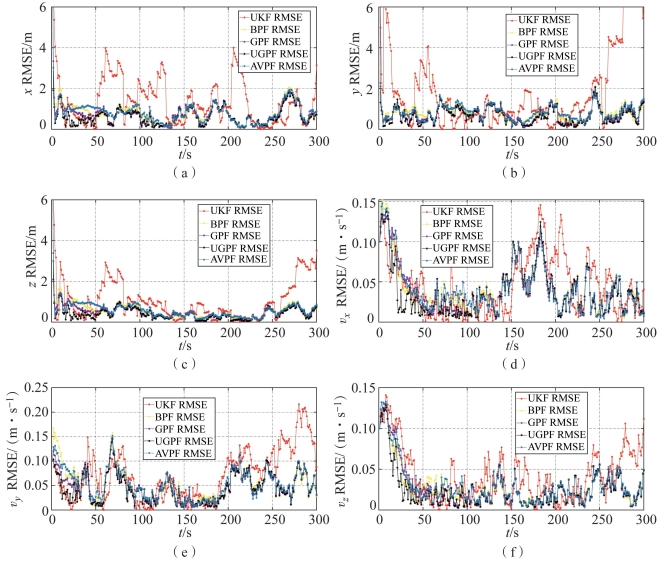
由于UKF精度较差，BPF、AVPF和GPF改为前10步由UGPF引导。仿真实验得到图3-19所示的RMSE曲线，各滤波算法的统计信息如表3-6所示。

(www.daowen.com)

图3-19　闪烁量测噪声下的RMSE曲线（见彩插）

（a）x轴位置的RMSE曲线；（b）y轴位置的RMSE曲线；（c）z轴位置的RMSE曲线；（d）x轴速度的RMSE曲线；（e）y轴速度的RMSE曲线；（f）z轴速度的RMSE曲线

表3-6　闪烁量测噪声下各滤波算法的统计信息

在闪烁噪声的作用下，4种粒子滤波就精度而言依旧能够较大程度地优于UKF。然而与BPF相比，AVPF在精度上的优势不明显，这似乎与前面的理论分析相悖。实际上，航天器相对运动具有低激励噪声的特点，本例中激励噪声的方差比量测噪声小一个数量级，这意味着图3-16中的先验密度比似然函数更为尖锐。在这种情况下，先验密度已经十分接近后验密度，即便出现量测野值，根据转移密度（也就是先验密度）生成粒子集的BPF和GPF也不容易出现严重的权值退化。基于以上原因，AVPF相对于BPF的精度优势未能体现出来，UGPF在精度上也只是小幅度地优于GPF。

闪烁噪声的概率密度是单峰的，GPF和UGPF的高斯近似仍然有效，这是两者精度比BPF、AVPF更高的前提条件。其中UGPF在GPF的基础上优化了粒子的分布，因此取得了比GPF稍高的精度，在计算成本上也小于BPF和AVPF。

现在通过ε的取值改变量测噪声的闪烁强度。ε分别取0.05、0.1和0.2，在同样的初值和噪声条件下进行蒙特卡罗仿真，得到的统计信息如表3-7所示。根据表3-7，可绘制图3-20所示的折线图。

表3-7　闪烁量测噪声下各滤波算法的统计信息

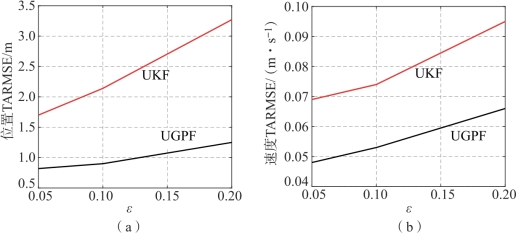
图3-20　UKF和UGPF的TARMSE随ε值的变化情况

（a）位置TARMSE；（b）速度TARMSE

显然，UGPF的精度始终高于UKF。此外，由图3-20可以发现，与UGPF相比，UKF对闪烁强度更为敏感：在ε增大时，UKF精度的下降幅度大于UG⁃PF。在一定的范围内，ε越大，闪烁噪声就越偏离高斯分布，这使得UKF的精度严重依赖于闪烁强度；而UGPF始终能够较好地逼近后验密度，故精度不会随着ε的增大而严重降低。事实上，UGPF的TARMSE也随着ε的增大而缓慢升高，这是因为ε的增大会使得闪烁噪声的方差增大，量测值随之变得不准确。