现考察在服从伽马（gamma）分布的量测噪声作用下各滤波器的性能。初值条件和激励噪声同表3-3，假设量测噪声满足

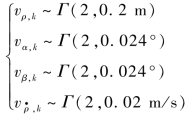
取粒子数N＝3 000，蒙特卡罗仿真次数NMC＝20，BPF、AVPF和GPF的前三步由UKF引导，得到如图3-15所示的RMSE曲线，其统计信息如表3-5所示。

gamma噪声的均值不为0，使得UKF产生了较大的估计误差。粒子滤波直接对后验密度进行逼近，理论上对噪声类型不敏感，因此在精度上未受到太大影响。由于gamma概率密度函数的计算较为复杂，各粒子滤波的计算成本均大幅度上升。尽管UKF估计误差较大，UGPF仍然在4种粒子滤波中以较低的计算量取得了最高的精度。若保持量测噪声的方差不变而将均值增大1倍，以图3-16所示的x轴位置RMSE曲线为例，可以明显地发现UGPF的精度降低到GPF以下。这是因为随着量测噪声均值的增大，UKF的误差进一步加大，对UGPF的粒子分布起到了误导的作用。

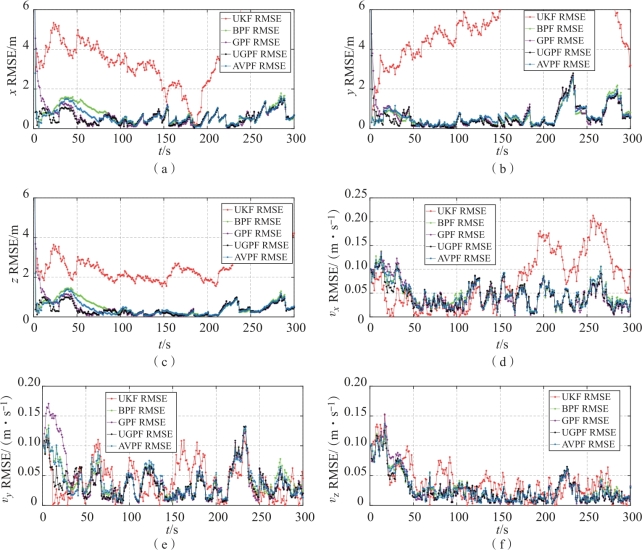
图3-15　gamma量测噪声下的RMSE曲线（见彩插）

（a）x轴位置的RMSE曲线；（b）y轴位置的RMSE曲线；（c）z轴位置的RMSE曲线；（d）x轴速度的RMSE曲线；（e）y轴速度的RMSE曲线；（f）z轴速度的RMSE曲线(www.daowen.com)

表3-5　gamma量测噪声下各滤波算法的统计信息

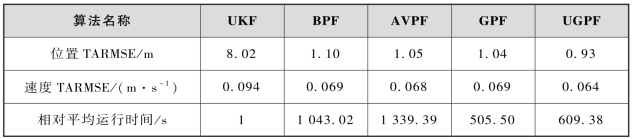
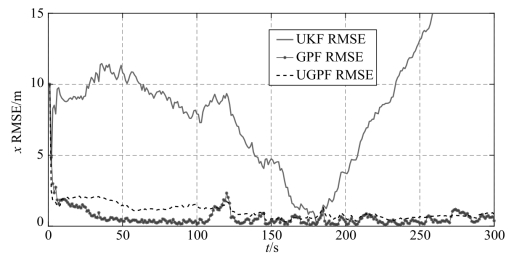
图3-16　加大gamma噪声均值后的RMSE曲线

考虑到gamma噪声的有偏性，实际上UKF的误差中有相当一部分是由量测噪声的偏差引起的。若对UKF进行偏差补偿，即在量测一步预测值的基础上叠加噪声均值，则有望减小UKF的误差，从而提高UGPF的精度。在前面将量测噪声均值增大1倍的基础上，对UKF进行偏差补偿，经过仿真得到图3-17所示的x轴位置RMSE曲线。与图3-16相比，UKF的RMSE大幅度降低，UGPF的精度也相应得到了提高，其TARMSE小于GPF。

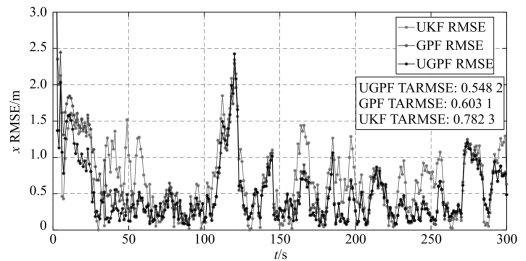
图3-17　经过对UKF进行偏差补偿的RMSE曲线（见彩插）