现假设雷达量测噪声服从高斯分布。仿真所使用的初值及噪声方差等条件如表3-3所示，其中激励噪声方差的大小是根据摄动力及控制力的不确定性选取的，量测噪声方差的大小则根据现阶段的雷达精度选取。

表3-3　仿真条件

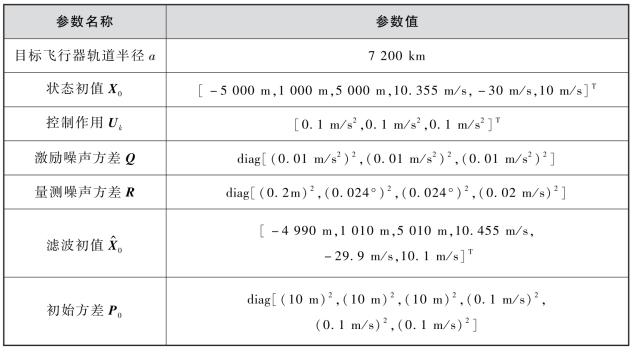
假设初始状态服从以为均值、以P0为方差的高斯分布。取粒子数N＝3 000，滤波步数NT＝300，相对轨道动力学模型离散化的时间间隔为T＝1 s，仿真实验得到图3-11所示的RMSE曲线。其中BPF算法含有MCMC步骤，位置和速度RMSE的单位分别为m和m／s。由图3-11可知，UKF的收敛结果与各粒子滤波一致，这说明航天器相对导航模型的非线性和非高斯特性并不强，4种粒子滤波与UKF均能较好地收敛到最优解附近。

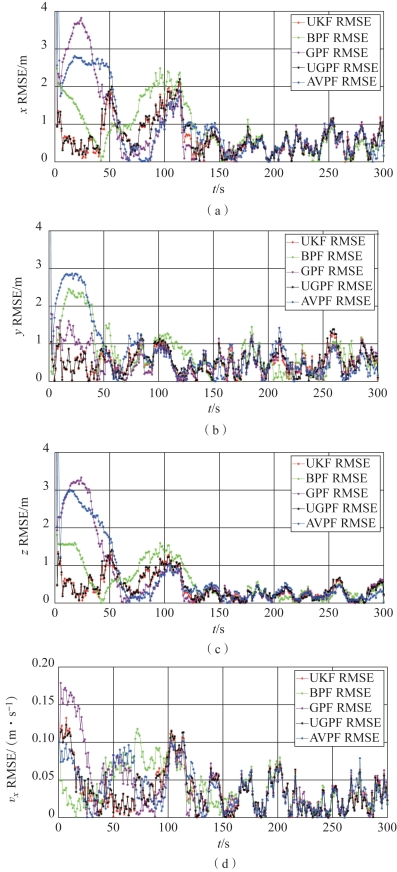
图3-11　高斯量测噪声下的RMSE曲线（见彩插）

（a）x轴位置的RMSE曲线；（b）y轴位置的RMSE曲线；（c）z轴位置的RMSE曲线；（d）x轴速度的RMSE曲线

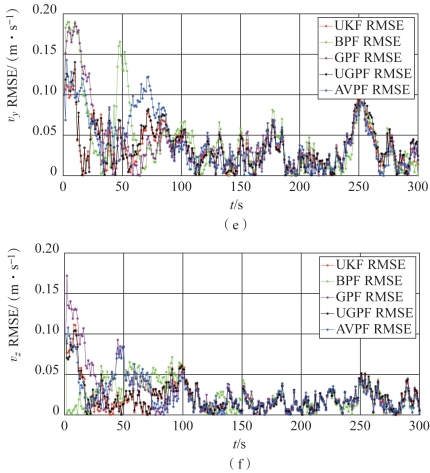
图3-11　高斯量测噪声下的RMSE曲线（续）（见彩插）

（e）y轴速度的RMSE曲线；（f）z轴速度的RMSE曲线

尽管各滤波算法在收敛后有着相似的精度，但它们的收敛过程却是不同的：由图3-11（a）、（b）、（c）可以明显发现，UKF和UGPF有着最快的收敛速度，而BPF、AVPF和GPF的收敛速度却较慢。

现对上述现象的原因进行分析。在滤波的初始时刻，由于初始方差阵较大，因此先验密度比较宽阔，生成的粒子集较为分散。对于这些粒子而言，只有落在状态真值附近的才能够具有较大的似然比，从而获得较大的权重。然而在本例中，滤波初值与真实状态初值存在着一定的偏差，初始方差阵也较大，这使得初始的粒子集里只有极少数粒子落在状态真值附近。粒子集的权值方差较大，便出现了权值退化问题。滤波初始时刻的权值退化示意图如图3-12所示。

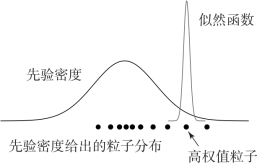
图3-12　滤波初始时刻的权值退化示意图

显然，仅靠个别高权值粒子无法有效表征后验密度。BPF和AVPF在重采样之后还会出现样本匮乏的问题，由于激励噪声的方差较小，只有经过若干次迭代才能够缓慢地收敛到最优解附近。粒子滤波稳定性的证明基于粒子数趋于无穷大的假设，但在实际应用中粒子数必然是有限的，滤波稳定性取决于初值条件及噪声大小。

通过仿真实验可以验证，在粒子数有限时，若减小滤波初值相对于状态真值的偏差，则BPF、AVPF和GPF的收敛会加快；若增大初始偏差，则BPF、AVPF和GPF的收敛会减慢，甚至导致滤波发散。UKF作为确定性采样滤波器，其稳定性与初值无关，这建立在严格的数学证明的基础上。UGPF利用UKF生成重要性密度，能够不受初始偏差的影响，使粒子集在UKF的指导下向高似然比区域移动，避免了权值退化的问题，滤波稳定性较好。(www.daowen.com)

使滤波初值的偏差增大1倍，同时将初始方差阵设置为原来的4倍，进行仿真实验，得到如图3-13所示的x轴位置RMSE曲线。由图可以发现，GPF收敛减慢，在第80 s左右才真正收敛，BPF在第100 s时仍未收敛，AVPF则呈现出发散的趋势。然而，UKF和UGPF在增大初值偏差和初始方差后却仍然具有较快的收敛速度（图中UKF和UGPF的RMSE曲线几乎重合）。

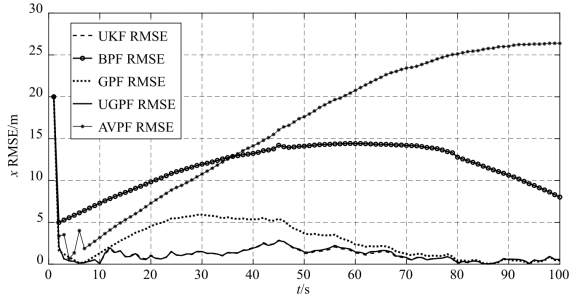
图3-13　高斯量测噪声下增大初值偏差和初始方差后的RMSE曲线

滤波器的稳定性是其能够正常工作的前提，若滤波器不稳定，滤波精度也就无从谈起。在实际情况下，真实的状态初值往往无法准确得知。由于初值的不确定性，初始方差通常也选取得较大。对于BPF、AVPF和GPF而言，理论上增加足够多的粒子能够改善收敛慢的问题。但是，考虑到计算成本，这并非一种理想的方法。若在前几步使用UKF进行滤波，在状态估计值和方差略加收敛之后再使用BPF、AVPF和GPF，则有望避免图3-11所示的收敛过慢的问题，这种做法称为“使用UKF引导”。初值和噪声条件仍按照表3-3选取，BPF、AVPF和GPF的前三步使用UKF引导，蒙特卡罗仿真次数为NMC＝20，得到如图3-14所示的RMSE曲线。

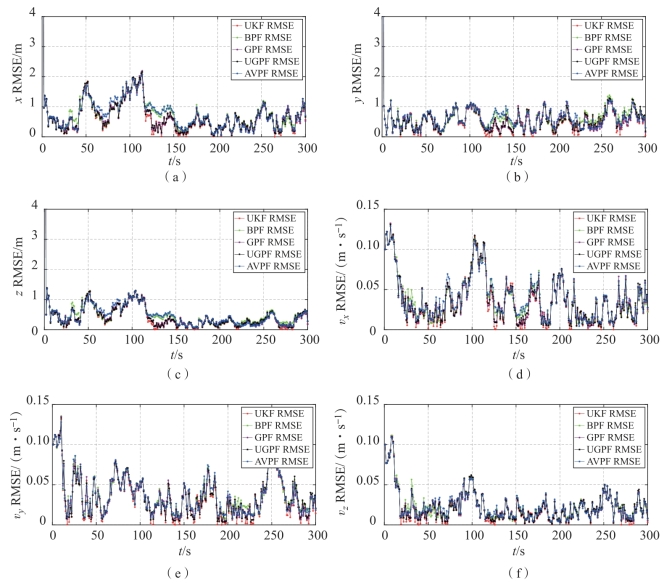
图3-14　高斯量测噪声下的RMSE曲线（BPF、AVPF和GPF经过UKF引导）（见彩插）

（a）x轴位置的RMSE曲线；（b）y轴位置的RMSE曲线；（c）z轴位置的RMSE曲线；（d）x轴速度的RMSE曲线；（e）y轴速度的RMSE曲线；（f）z轴速度的RMSE曲线

观察图3-14可发现，在前三步由UKF引导后，BPF、AVPF和GPF收敛加快。为方便定量比较各滤波算法的精度，定义位置TARMSE可以表示为

速度TARMSE可以表示为

则可得到图3-14中RMSE曲线的统计数据，如表3-4所示。

表3-4　高斯量测噪声下各滤波算法的统计信息

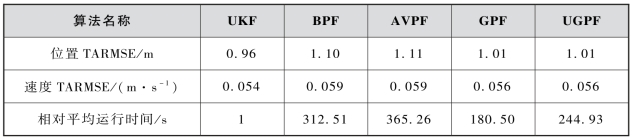
由表3-4可知，由于相对导航模型的非线性、非高斯特性较弱，UKF已经十分接近最优解，粒子滤波在精度上很难再比UKF有提高。限于粒子数，4种粒子滤波的精度反而不如UKF。GPF和UGPF的高斯假设有效，由于彻底免去了重采样步骤及其带来的样本匮乏问题，因此与BPF和AVPF相比，GPF和UGPF有着更高的精度和更低的计算量。UGPF在每步滤波中均需要调用一次UKF，并且权值计算较为复杂，故计算成本高于GPF。