假定某系统的状态方程和量测方程分别为

现根据该一维非线性算例比较并分析粒子滤波与高斯滤波的性能。假设零均值高斯白噪声wk和vk的方差分别为10和1，初始状态真值为0.1，滤波初值为0.1，初始方差为10。各粒子滤波的粒子数均取为N＝100，其中BPF含有MCMC步骤。由于粒子滤波存在着随机性，因此共进行NMC＝50次蒙特卡罗仿真，以获取各算法的统计信息。

仿真完毕后，使用均方根误差（Root Mean Square Error，RMSE）来量各滤波算法的精度。状态xk处RMSE的计算公式为

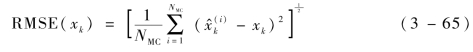
式中：xk为状态真值；为滤波算法在第i次仿真中对该状态的估计值。

为了定量描述滤波算法在总体上的精度，定义平均RMSE（Time-averaged Root Mean Square Error，TARMSE）为

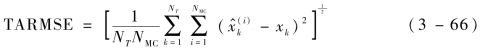
式中：NT为一次蒙特卡罗仿真的步数。

为了衡量各算法的计算成本，定义平均运算时间为

式中：为第i次蒙特卡罗仿真中在第k步的运算时长。

为了方便比较，再定义相对平均运算时间为各滤波算法与UKF的平均运算时间之比。

通过仿真，得到图3-6所示的RMSE曲线及表3-1给出的统计数据。由表3-1可知，在估计精度上，BPF和AVPF优于UKF，而GPF和UGPF反而不如UKF。这是由于在给定的量测模型下，具有双峰特性的后验密度与高斯分布相差很大，故基于高斯假设的UKF、GPF和UGPF的估计精度较低。BPF和AVPF没有类似的假设，在理论上能够逼近任意形式的后验密度，所以估计精度较高。此外，由于激励噪声较大，AVPF相对于BPF的优势不明显。在时间成本上，粒子滤波的运算时间远大于UKF，仅100个粒子便使得粒子滤波的计算量超出UKF近30倍。

图3-6　一维算例中各算法的RMSE曲线（见彩插）

表3-1　一维算例中各算法的统计数据(www.daowen.com)

取粒子数N＝10 000，根据BPF绘制前10步滤波的粒子分布，如图3-7所示，图中竖轴代表某个区间段内的粒子数n（x）与总粒子数N之比。取出第二个时刻的粒子分布，如图3-8所示。经过核平滑函数的拟合和归一化，可得到k＝2时刻的后验概率密度近似曲线，即图中的粗实线。从图3-7和图3-8中可以很明显地观察到后验密度的双峰特性，这体现了粒子滤波逼近后验密度的能力，也验证了前面的分析。为了便于可视化，图3-7和图3-8中取了不同的组宽度。

图3-7　一维算例中前10步滤波的粒子分布

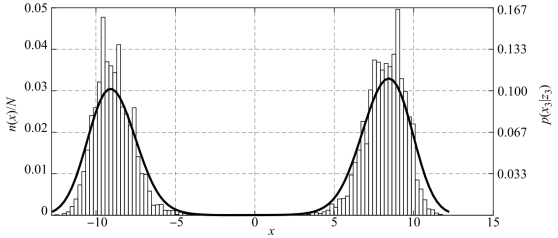
图3-8　一维算例中k＝2时刻的粒子分布及后验密度曲线

若将算例中的量测方程修改为

在相同的条件下再次进行仿真试验，可得到如图3-9所示的RMSE曲线。为了体现各算法RMSE曲线的特点，将纵坐标截取在区间［0，20］内。各曲线的统计信息如表3-2所示。

图3-9　一维算例中各滤波算法的RMSE曲线（修改量测模型后）（见彩插）

表3-2　一维算例中各滤波算法的统计信息（修改量测模型后）

式（3-68）中的量测方程虽然仍属于非线性模型，却使状态的后验密度由双峰变为了单峰。显然，在修改量测模型后，GPF和UGPF的精度得到大幅度的提高，这是因为用高斯分布近似单峰分布比近似双峰分布更为有效。根据BPF作出前10步滤波中的粒子分布如图3-10所示，以验证后验密度的单峰特性。

图3-10　一维算例中前10步滤波的粒子分布（修改量测模型后）