扩展卡尔曼滤波对非线性方程进行线性化，从而近似非线性函数。与扩展卡尔曼滤波相比，无迹卡尔曼滤波采用了一种完全不同的方法：利用加权样本点逼近系统状态的概率密度。无迹卡尔曼滤波的理论基础在于逼近任意函数的概率分布比直接逼近任何非线性函数更容易，其实现方式是无损（UT）变换。

3.3.4.1　无损变换

假设X为一个n维的随机向量，其均值和协方差分别为和P。X经非线性向量函数的变换后，得到Y，UT变换的目的在于求取Y的均值及协方差Py。无损变换的步骤如下：

（1）构造离散样本点（sigma点）并计算相应的权值。构造样本点的原则是保证样本点的均值和协方差与原变量一致。其核心问题是确定采样策略，并且关系到对非线性系统的近似精度。不同的采样策略会产生不同的变换采样点，计算得到的均值和方差等信息也不同。这里主要介绍采用比例对称采样策略的无损变换。

根据比例对称采样策略，得到的采样点为

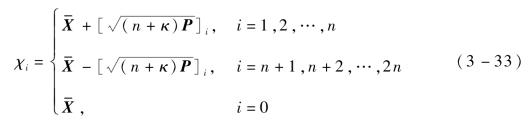
式中：下标“i”表示矩阵的下三角分解的平方根的第i列。

用于计算均值和方差的样本权值分别为

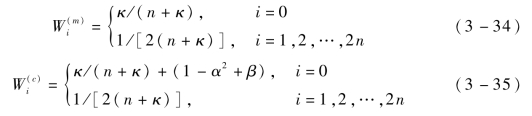
式中：n为状态变量X的维数；α控制采样点的状态分布，确定sigma点在周围分布，通常取一个小的正常数（104≤α≤1）；κ为比例系数，用于调节采样点与之间的距离，一般取0或3-n；β为状态分布参数，对于高斯分布，β取2。

（2）将构造的sigma点集｛χi｝代入f（·）进行非线性变换，得到变换后的sigma点集：

｛γi｝即可近似地表示Y＝f（X）的分布。

（3）计算非线性变换后的sigma点集｛γi｝的均值和方差。利用式（3-34）和式（3-35）对｛γi｝进行加权处理，得到Y的均值和方差：

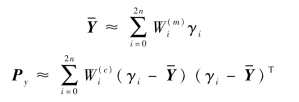
3.3.4.2　无迹卡尔曼滤波算法

UT变换避免了对非线性函数进行线性化近似，意味着即使系统的非线性程度比较高或者系统模型比较复杂，算法的复杂度也不会增加。同时，由于UT变换不需要计算导数，因此可用于系统模型存在不连续点的情况。UT变换和EKF算法对非线性系统的近似原理如图3-4所示。

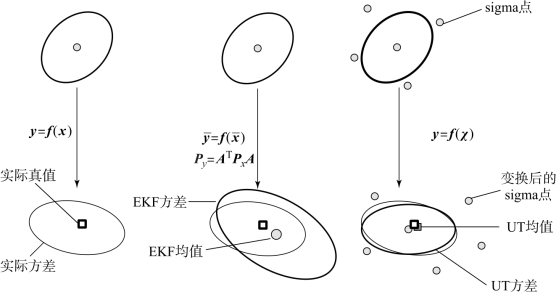
图3-4　非线性变换原理

（a）真实情况；（b）EKF原理；（c）UT变换原理(www.daowen.com)

下面介绍基于UT变换的无迹卡尔曼滤波算法。假设某系统由如下的非线性离散状态空间方程描述：

则利用无损变换对式（3-36）所示系统进行卡尔曼滤波的步骤如下：

（1）计算sigma点。采用比例对称采样，sigma点的均值和协方差为前一时刻的估计值和前一个时刻的估计均方误差Pk-1，即得采样点为

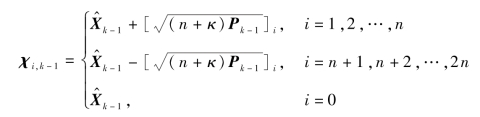
（2）对｛χi，k-1｝进行f（·）非线性传播，并计算非线性变换后sigma点集｛χi，k｜k-1｝的均值和协方差。均值即对应状态一步预测值，协方差对应一步预测均方误差：

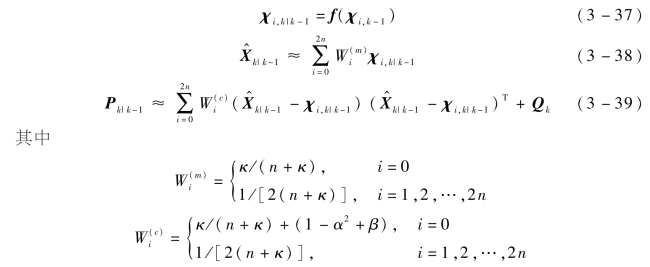
（3）对｛χi，k｜k-1｝点集进行h（·）的非线性变换，并计算变换后点集｛γi，k｜k-1｝的均值和协方差：

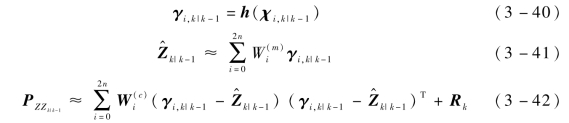
（4）量测更新。计算滤波增益：

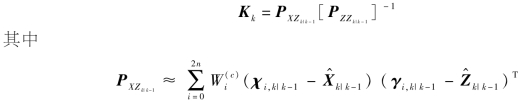
（5）输出状态估计信息。状态滤波方程为

状态滤波均方误差矩阵为

上述5个步骤即UKF滤波算法的迭代流程，如图3-5所示。

从图3-5中可以看出，UKF算法也分为时间更新和量测更新过程，具有和卡尔曼滤波相同的算法结构，因此不需要对卡尔曼滤波流程进行较大的改动。

UKF直接使用系统的非线性模型，对其概率密度分布进行近似，至少能够达到二阶精度；UKF避免了求取系统状态空间模型的雅克比矩阵，对于不可微的系统同样能够进行状态估计。

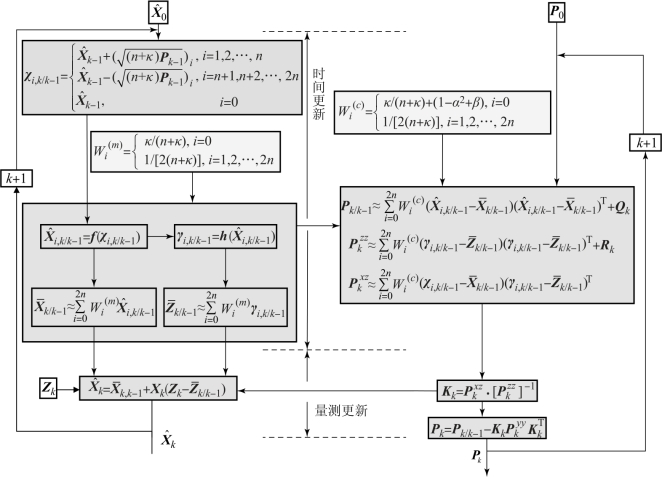
图3-5　UKF迭代流程