在k时刻获得最新的量测值Zk后，可利用其对状态一步预测概率密度进行修正，得到当前状态Xk的后验概率密度：

式中：p（Zk｜Z1：k-1）为归一化常数。

递推贝叶斯估计的流程如图3-1所示。对贝叶斯估计的时间更新和量测更新进行循环，便可递推地得到每一时刻系统状态的后验概率密度p（Xk｜Z1：k）。该概率密度包含了Xk的所有统计信息，因此根据它可得到Xk的均值、方差以及峭度、斜度等任意阶统计量。上述信息的估计可统一表示为

当Ω（Xk）＝Xk时，可得最小均方误差（Minimum Mean Square Error，MMSE）意义下的最优估计它又称为最小均方误差估计子。(www.daowen.com)

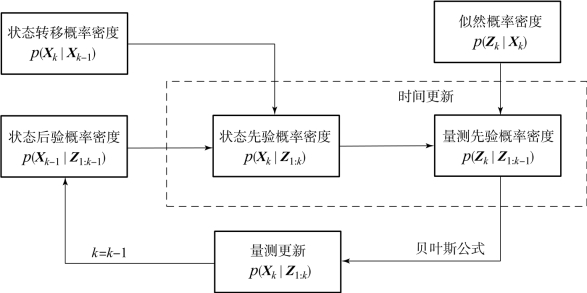
图3-1　递推贝叶斯估计示意图

当式（3-1）和式（3-2）所描述的系统模型、量测模型满足线性关系，并且初始状态、系统噪声、量测噪声均满足独立的高斯分布时，状态一步预测概率密度函数和后验概率密度函数亦满足高斯分布，该分布由状态量的均值和方差唯一确定。此时，式（3-9）所描述的精确解是解析的，并且为一个线性估计子，这便是著名的卡尔曼滤波。

在大多数条件下，系统DSS模型为非线性的，状态初值和噪声也难以满足理想的高斯分布。此时，贝叶斯理论给出的最优解不再解析，且随着时间的推移需要无穷多个参数描述，对计算能力和存储容量提出了较高要求，甚至根本无法实现。在这种情况下，人们转而寻找贝叶斯估计问题的次优解。解决上述问题的思路通常可以归结为以下两种：

（1）尽管该情况下卡尔曼框架不再是最优的估计子，但是仍然可以将其作为次优解使用。该估计方法只需要系统状态前两阶矩的统计信息，并假设所求的后验密度满足高斯分布，因此统称为高斯滤波。这类方法有基于雅可比线性化的扩展卡尔曼滤波（Extended Kalman Filter，EKF）、基于无迹变换的无迹卡尔曼滤波（Unscented Kalman Filter，UKF）、基于Stirling插值公式的均差滤波（Divided Difference Filter，DDF）、中心差分滤波（Central Difference Filter，CDF）和基于数值积分方法的高斯-厄米特滤波（Gauss-Hermite Filter，GHF）等。

（2）直接通过数值方法逼近贝叶斯估计问题的最优解，即后验概率密度此类方法有栅格法（Grid-Based Methods，GBM）、近似栅格法（Approximate GBM）、矩近似法（Moment Approximation Methods，MAM）和以粒子滤波（Particle Filter，PF）为代表的蒙特卡罗（Monte Carlo）方法等。