以上4种编队构型均基于参数方程式（2-164）设计，结构简单，数学描述非常清晰，但它们均无法实现对坐标原点即主航天器的环绕飞行。对于实际中大量存在并且需求迫切的绕飞任务，必须寻找稳定而有效的绕飞构型。

可以将平面内的环绕轨迹定义为原点位于轨迹曲线的内部，空间环绕轨迹则可相应定义为轨迹曲线在各坐标面的投影均为平面环绕轨迹。但是鉴于周期轨迹的单参数方程的复杂性，其坐标形式的方程通常很难给出，直接讨论一般性的环绕条件在数学上并不方便，而且也不是必要的，因为工程上总会期望环绕轨迹是相对规则的。考察相对运动周期解式（2-108），可以看出轨道面内的相对运动具有一定的近似椭圆特性。

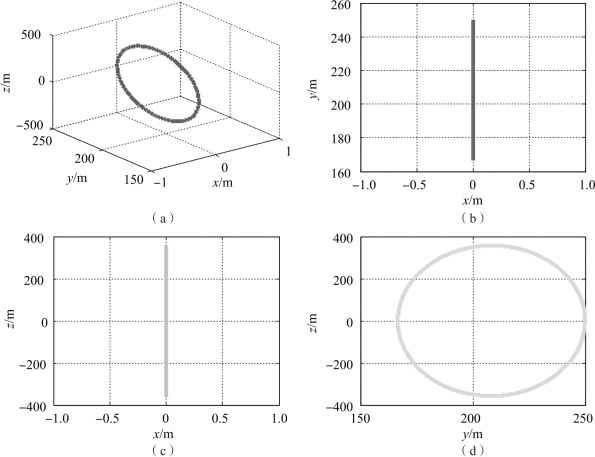
图2-11　水平面椭圆编队构型

（a）水平面椭圆编队空间轨迹；（b）水平面椭圆编队空间轨迹在xoy平面投影；（c）水平面椭圆编队空间轨迹在xoz平面投影；（d）水平面椭圆编队空间轨迹在yoz平面投影

作如下变换：

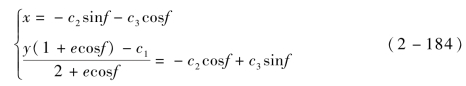
进一步可得

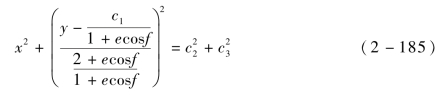(www.daowen.com)

当e＝0时，式（2-185）即表示一个椭圆；当e→0时，式（2-185）描述的曲线就越接近椭圆。将x＝0和y＝0代入其中，可得原点在曲线内部的条件为

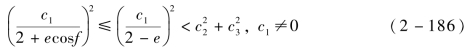
当c1＝0时，式（2-186）显然成立。称满足式（2-185）和式（2-186）的相对周期轨迹为轨道面绕飞轨迹，第3章将基于此构型设计编队初始化的控制器。

仿真算例：取主星轨道根数为

从星初始相对状态使得各积分常数满足c1＝200，c2＝150，c3＝350，以及c5＝c6＝220。可得轨道面绕飞编队构型如图2-12所示。

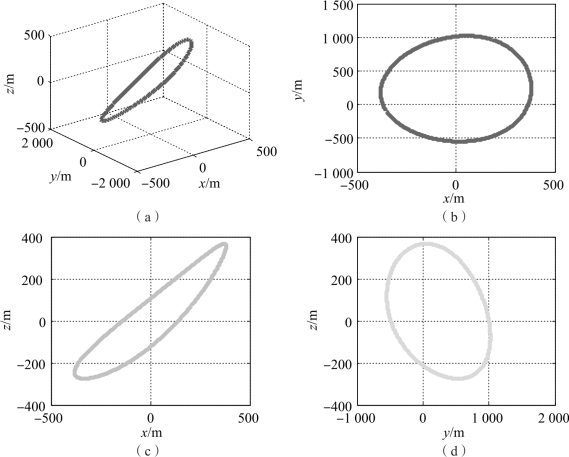
图2-12　轨道面绕飞编队构型

（a）轨道面绕飞编队空间轨迹；（b）轨道面绕飞编队空间轨迹在xoy平面投影；（c）轨道面绕飞编队空间轨迹在xoz平面投影；（d）轨道面绕飞编队空间轨迹在yoz平面投影