鉴于椭圆轨道相对运动的周期性条件较为复杂，本节将采用仿真的方式验证这一结果的准确性。必须说明的是，式（2-104）是线性化相对运动T-H方程式（2-75）的精确周期性条件，但这里将基于未做任何线性近似处理的无摄完整相对动力学式（2-49）进行仿真，以更进一步地验证在ρ≪rt的条件下周期条件式（2-104）的数值精确性。求解非线性方程式（2-85）的数值解使用四阶龙格-库塔法。

设某一时刻主航天器的轨道根数为即主航天器运行于一条地球同步轨道。从航天器初始相对状态为

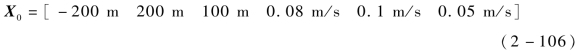
由轨道动力学可以计算得到从航天器的轨道根数与惯性状态。此种初始相对状态对应的c4＝-967.904 6，仿真两个主航天器轨道周期，可得相对运动轨迹如图2-5所示，星号表示初始位置，显然这并不是一个周期轨道。依据式（2-104）重新设计初始的y向速度为vy0＝0.039 9 m／s。同样，仿真两个主航天器轨道周期，可得相对运动轨迹如图2-6所示。从图中可以看出，这是一个相对规整的周期封闭轨迹，从而验证了2.5.3节推导的周期相对运动初始条件的正确性。(www.daowen.com)

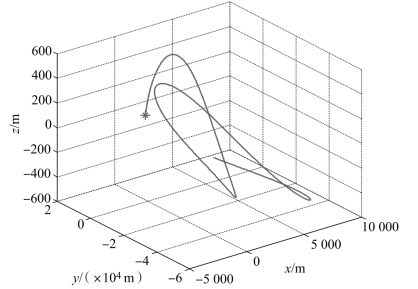
图2-5　未修正的相对运动轨迹

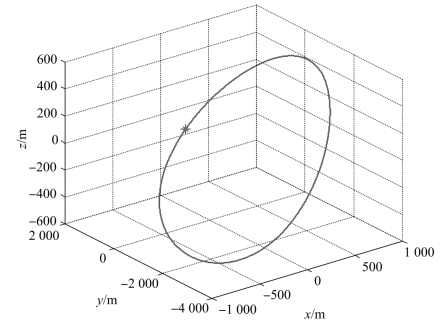
图2-6　满足周期初始条件的相对运动轨迹