【摘要】:单脉冲交会的主要特点是要求原轨道与目标轨道相交。但是,当原轨道与目标轨道无交点时,则单脉冲无法实现与目标航天器的变轨交会,此时脉冲次数至少要增加到两次。当潜伏轨道与目标轨道都为椭圆轨道时,双脉冲霍曼变轨交会是双脉冲变轨交会中燃料最优的变轨形式。
单脉冲交会的主要特点是要求原轨道与目标轨道相交。但是,当原轨道与目标轨道无交点时,则单脉冲无法实现与目标航天器的变轨交会,此时脉冲次数至少要增加到两次。当潜伏轨道与目标轨道都为椭圆轨道时,双脉冲霍曼变轨交会是双脉冲变轨交会中燃料最优的变轨形式。一般来说,霍曼交会要求目标航天器的轨道半径大于追踪航天器轨道半径。假设目标航天器的轨道半径为r0,观测航天器的轨道半径为r1(图2-3),变轨过程中的两次脉冲方向分别为内圆轨道和外圆轨道的切向方向,其过渡轨道为椭圆轨道,过渡轨道的近地点和远地点分别位于两次脉冲的发生位置。
由航天器速度计算公式可以得到两次脉冲大小分别为过渡轨道近地点和远地点与内外圆轨道的速度之差,其计算公式分别为
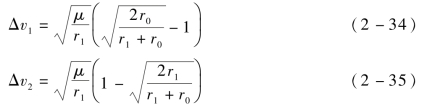
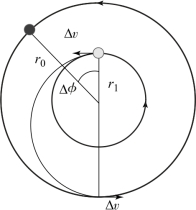
图2-3 双脉冲霍曼交会(https://www.daowen.com)
事实上,要实现两个航天器的交会,还必须有严格的交会时刻限制,即交会机动开始时刻,两个航天器的相角差必须严格等于Δφ,Δφ的值可计算如下:
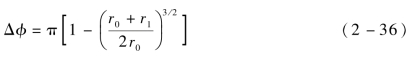
若得到变轨指令开始时刻两个航天器的相角差刚好为Δφ,则整个交会时间刚好为过渡椭圆轨道的半个周期。实际上,得到变轨指令时刻不可能刚好相角差为Δφ,记初始时刻相角差为Δφ+Δφ′。因此,追踪航天器还必须在轨道上等待一段时间来消除Δφ′,这样整个轨道交会的时间消耗为
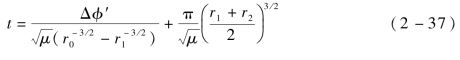
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章







