回归分析有不同的类型：按自变量的个数分，有一元回归和多元回归；按回归图线的形状分，有线性回归和非线性回归。其中，一元线性回归分析是最基本的类型，它分析的依据是一元线性回归模型。

一元线性回归模型是根据两变量的相关方向和线性形态拟合的反映两个变量之间平均变化关系的标准直线。当两变量之间为单向因果关系时，线性回归模型为yc＝a＋bx；当两变量之间互为因果关系时，线性回归模型有两个：一个是y倚x型，即yc＝a＋bx；另一个是x倚y型，即xc＝c＋dy。

拟合线性回归模型的条件：一是两变量之间确有显著相关关系（经过相关系数r值验证）；二是两变量的相关形态确实接近直线（经过散点相关图验证）。只有同时满足这两个条件才能配合回归直线。

（一）线性回归模型的参数估计

如果在相关分析中，证明自变量x和因变量y符合线性显著相关的条件，即可拟合以下y倚x的线性回归模型：

式中：yc表示因变量y的估计理论值；x为自变量的实际值；a、b为待定参数。参数a、b的数学意义——a是直线方程的截距，b是直线的斜率。其经济意义——a是当x为零时，y的初始值；b是当x每增加一个单位时，y平均增加的数量，b也叫回归系数。

我们知道，根据两变量的线性散点轨迹可拟合许多条直线，但回归分析的目的则是为了找到一条最优直线。数理统计证明，用最小平方法配合的反映两变量变化规律的线性模型最优、最具代表性。

最小平方法是依据偏微分求极值的原理来推算两参数a、b的。用最小平方法拟合的直线须同时满足以下两个条件：

（1）∑（y－yc）＝0，即实际值y与理论值yc的离差和等于零。

（2）∑（y－yc）2＝最小值，即实际值y与理论值yc的离差平方和等于最小值。

设：Q＝∑（y－yc）2＝∑（y－a－bx）2

按照偏微分求极值的原理，要使Q达到最小值，须满足Q对参数a、b的偏导数等于零，以建立联立方程组，然后求得a、b两值。即

分别求偏微分并使其等于零：

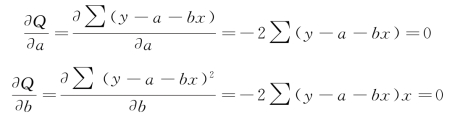
对方程组简化：

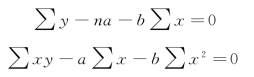
求解两参数为

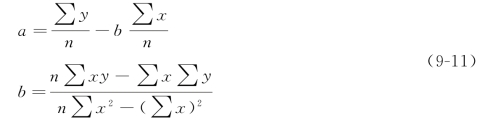
如果分析的对象是两变量的相关分配数列，参数a、b的求解式相应为

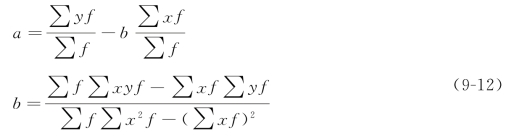
例9-3 承例9-1某市城镇居民人均年收入与日用品销售额资料表9-3，通过相关分析知r＝0.9813，表明该市城镇居民人均年收入与日用品销售额之间存在高度正相关关系。试根据资料建立日用品销售额（y），居民人均年收入（x）的线性回归方程，并预测当居民人均年收入达到10000元时，该市日用品销售额的估计值？

通过表9-4的资料汇算知：

设居民人均年收入与日用品销售额的线性回归方程为yc＝a＋bx

将汇算数据代入式（9-11）可得a、b参数值。

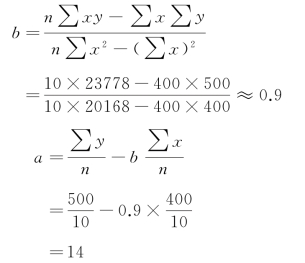
则居民人均年收入与日用品销售额的回归方程为yc＝14＋0.9x

当x＝100百元时yc＝14＋0.9×100＝104（亿元）。

即当居民人均年收入达到10000元时，该市日用品销售额的估计值为104亿元。

例9-4 承例9-2某企业连续30个月的产品单位成本与各月利润额的变动资料表9-4，通过相关分析知r＝－0.9957，表明该企业产品单位成本与各月利润额之间存在高度负相关关系。试根据资料建立利润额（y）倚产品单位成本（x）的线性回归方程，并预测当产品单位成本达到30元时，该企业月平均利润额的估计值为多少？

通过表9-4的资料汇算知：

设产品单位成本与各月利润额的线性回归方程为yc＝a＋bx(www.daowen.com)

将汇算数据代入公式（9-12）可得a、b参数值。

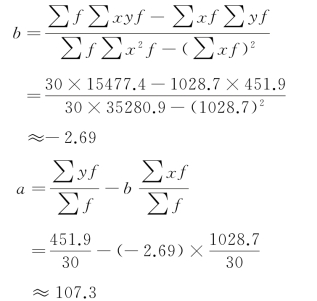
则产品单位成本与各月利润额的回归方程为yc＝107.3－2.69x

当x＝30（元）时，yc＝107.3－2.69×30＝26.6（百万元）。即当产品单位成本达到30元时，该企业月平均利润额的估计值为2660万元。

（二）估计标准误差

回归直线是反映两个变量之间一般数量关系的平均线，其作用在于根据自变量的已知值去推测因变量的估计值或平均值。这个估计值与实际值可能不一致，或大或小会产生一个误差，因而就有一个估计值的代表性问题。也就是线性模型的代表性有多强，准确性有多大的问题。

根据数理统计知识，回归方程的代表性一般是通过估计标准误差指标的大小来进行检验和说明的。估计标准误差是用来反映回归方程代表性大小的统计分析指标，也就是实际值与估计值的平均误差。估计标准误差一方面说明实际值与理论值之间离差的大小，另一方面通过回归误差说明回归直线代表性的大小。它与标准差有所不同，标准差是说明平均数代表性的，而估计标准误差是说明回归直线代表性的。估计标准误差越大，回归方程的代表性越弱；估计标准误差越小，回归方程的代表性就越强。所以，估计标准误差又叫回归标准差。其计算原理与标准差基本相同。计算公式为

式中：Sxy——表示y倚x回归方程的估计标准误差；

　　　yc——根据y倚x的回归方程推算出来的因变量的估计值；

　　　（n－2）——自由度。在一元线性回归中，由于计算了a、b两个参数，所以估计回归直线时失去了两个自由度。

在实际应用中，要求样本容量足够多，一般是n≥30。只要样本容量足够多，计算估计标准误差时就可以用n代替（n－2）来分析。这样，计算公式可变换为

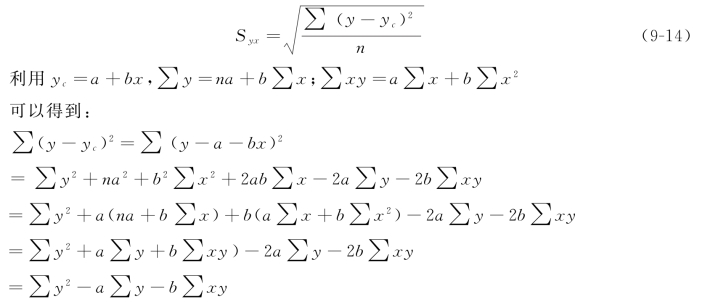
所以，估计标准误差的计算公式又可以简便地表述为

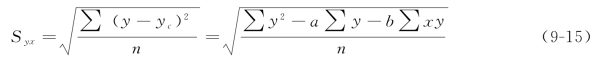
如果分析的对象是两变量的相关分配数列，估计标准误差的简便计算公式相应为

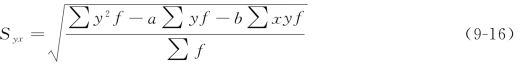
如上例9-4所示，已知：

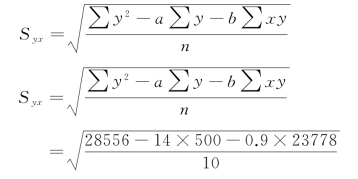
代入公式（9-15）得居民人均年收入与日用品销售额回归直线的估计标准误差为

（三）相关系数、回归系数和估计标准误差之间的关系

1.相关系数和回归

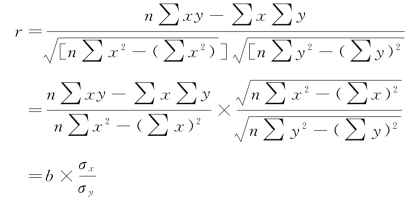
则相关系数和回归系数具有符号一致性的关系：

从上述关系可以看出：当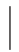r趋近于1时，两变量之间属高度相关关系，而估计标准误差Syx则趋近于0；当r趋近于0时，两变量无线性相关关系，估计标准误差Syx则趋向最大值，此时拟合的回归模型无实际意义。应用相关分析与回归分析应注意下面几个问题。

1.定性分析应作为相关分析与回归分析的前提

相关和回归的研究对象是具有相关关系的变量，如果研究对象没有相关关系，或相关关系不密切，进行相关和回归研究就没有实际意义。只有在确认现象间具有显著相关关系才能得出科学结论。现象是否具有相关关系是由其内在性质决定的，这就要求我们要以扎实的专业理论知识和丰富的实践经验为依据，先做好定性分析，确认所要研究的对象确实存在着相关关系以后，才能运用相关和回归分析法进行定量分析。

2.要注意相关分析和回归分析的应用范围和条件

根据部分实际资料建立起来的回归方程，是对过去阶段性经验的总结和概括。因此，回归估计和预测有个应用范围和应用条件的问题。在现有资料范围内，变量呈线性相关，超出了这个范围则不一定是线性的了，即使是线性相关，其待定参数也可能发生了变化。所以，相关分析和回归分析的成果不能应用到变量范围之外。同时，回归方程的建立是在具体资料条件下形成的，在应用回归方程进行估算时，必须考虑应用条件的变化，时过境迁，必然导致结论失误。

3.要将相关系数、回归模型和估计标准误差综合运用

相关系数的大小说明了变量之间有无相关关系及相关的密切程度，回归模型反映了变量之间平均变化的一般规律，估计标准误差则揭示了回归模型的代表性和估计预测的准确性问题。在相关和回归分析中，只有把这三个方面综合运用，才能使我们更全面、更准确地认识现象发展变化的规律。