相关表和相关图只能大体上判断变量之间的相关关系，而不能准确反映相关的密切程度。鉴于此，还需进一步研究用明确的统计分析指标来判定。

可以这样分析：两变量之间的相关关系是建立在两变量值变异情况比较上的，就是说，变量x与其平均数的离差和变量y与其平均数的离差（y－y）是否具有某些程度的“一致性”。两变量之间的变化具有“一致性”，说明两者具有相关关系，反之否定。且“一致性”越强，相关关系越密切。

通过两变量与各自平均值的离差资料来分析x、y两变量之间的相关关系，较早的方法是计算符号系数。其原理是把两个同平均值的相关离差数列做对称比较。如果一个数列的离差与另一个数列的离差有很多同号，就认为这两变量之间存在正相关；如果大多数为异号，就认为它们之间存在负相关；当与平均值离差的同号与异号大体一样时，就判定为不存在相关关系，或者认为相关关系极微弱。符号系数能帮助我们了解相关方向和相关的大体程度。其计算公式如下：

式中：∑A表示离差同号次数和；∑B表示离差异号次数和。

显然，符号系数从－1到＋1之间取值。当k＝－1，即所有离差符号都不一致时，就可以说变量之间的相关是负相关；当k＝＋1，即所有离差符号都一致时，就可以说变量之间存在正相关；当k＝0时，就说明两变量不存在相关关系。符号系数的优点在于意义明了，计算方便；其缺点在于掩盖了离差绝对值上的不同，指标只能反映相关的一般趋势。数理统计证明，测定变量之间相关密切程度的比较科学的指标是相关系数。

在各种相关关系中，单相关是基本的相关关系，它是复相关和偏相关的基础。单相关有线性和非线性相关两种表现形式。测定线性相关系数的方法是最基本的相关分析，是测定其他相关系数方法的基础。我们着重研究线性的单相关系数。

相关系数同样以两变量与各自平均值的离差为基础，进而用离差乘积的形式来反映变量之间的相关程度，所以又叫积差法相关系数。其基本计算公式如下：

用相关系数r来判定相关关系，首先要理解公式中协方差和变量标准差的意义。

1.标准差σx和σy的意义

本来协方差可足以揭示两个变量间的线性相关关系。那么为什么在r的计算公式中又将协方差除以σxσy呢？我们来对相关系数进行变换：

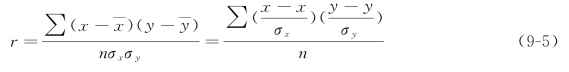
结果表明，相关系数实质上是变量x、y与其平均值的离差分别以各自标准差为尺度进行标准化后，针对标准量求得的协方差。经过离差标准化后再求协方差，有两个方面的意义：

（1）协方差是名数。不同现象的计量形式和变异情况不尽相同，相关程度不能直接以协方差大小加以比较。而经过标准化后协方差就化为了无名数，就可以对不同现象相关程度的高低进行比较。(www.daowen.com)

（2）协方差的数值范围不易确定。但将变量离差标准化后得到的相关系数的绝对值则不超过1，即相关系数在－1与＋1之间取值，这里不再证明。

现将相关系数的判定性质总结如下：

③当r＝0时，表示变量x与y之间不存在线性相关关系。

④当r＞0时，表示变量x与y正相关；当r＜0时，表示变量x与y负相关。

在统计实践中，直接利用相关系数的基本公式进行r的计算相当烦琐，因此我们对公式（9-4）做如下简化：

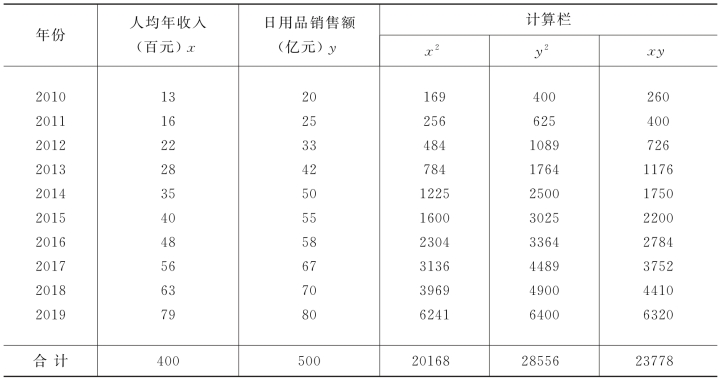
例9-1 某市城镇居民人均年收入与日用品销售额资料如表9-3所示。试分析两者的相关关系？

通过资料汇算可知：

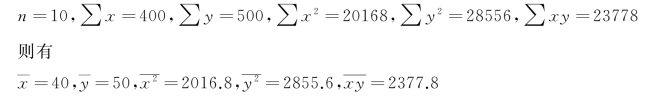
代入公式（9-7）可得

计算结果r＝0.9813表明：该市城镇居民人均年收入与日用品销售额之间存在高度正相关关系。即一般来讲，人均年收入越高，其购买力越强，日用品的销售额就越大；反之就越小。

表9-3　某市城镇居民人均年收入与日用品销售额资料