从上述实例的测算可以看出无论是拉氏公式还是派氏公式的计算结果都是具有一定经济含义的。从理论上来讲都是可行的，但在实际运用中就有个比较选择问题。在此，分别就数量指标指数和质量指标指数中拉氏公式与派氏公式的特点进行比较，然后选择其中较好的两个公式作为计算综合指数的常用公式并归纳出指数计算中同度量因素确定的两个基本原则，这两个原则贯穿于指数计算的始终，至今成为约定俗成的原则。其比较内容如表7-2、表7-3所示。

表7-2　数量指标指数的对比

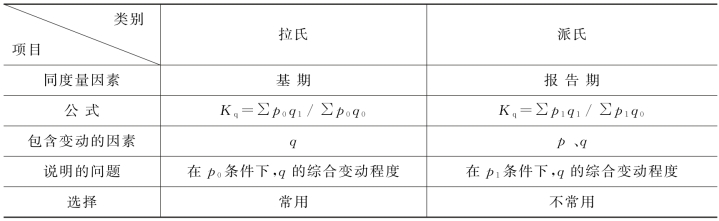
表7-3　质量指标指数的对比

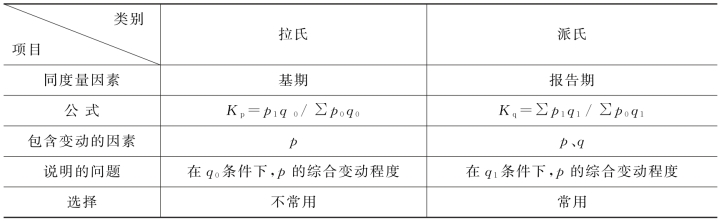
从表7-2可以看出：一般地选择拉氏数量指标指数公式来计算数量指标的综合变动程度，若概括为一般的原则即是：数量指标指数要以基期的质量指标为同度量因素。其原因是该公式可以单纯地反映数量指标的变化，不包括质量指标变动因素的影响。派氏数量指标指数公式之所以包括p、q共变因素，这可以借助于对其公式的分解而一目了然。

公式分解如下：

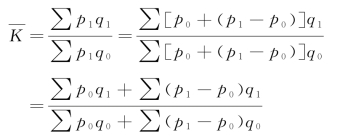
从表7-3中对比可以看出：一般地选择派氏质量指标指数来计算质量指标的综合变动。若概括成一般的原则，即质量指标指数要以报告期的数量指标为同度量因素。虽然派氏质量指标指数也包括同度量因素本身的变动，或者说是包括p、q共变的因素，这也可以根据上述派氏数量指标指数类似的分解方法分解出派氏质量指标指数的共变影响部分，但我们可以有更充分的理由认为选择派氏质量指标指数更好，其原因有下面两个。

第一，派氏质量指标指数更具有实际意义。从理论上讲，为了单纯地反映质量指标（如价格的变动），应当把数量指标（如销售）量固定在基期，但从实际效果看，将销售量固定在报告期，可以反映由于价格变动产生的现实影响。因为人们更关心在报告期水准下由于价格变动需多支出多少，故选用该公式更具有实际意义。

第二，指数体系的要求。指数体系问题详见本章第五节，从中我们可以看出在指数体系中，其中一个因素指数的同度量因素固定在基期，则另一个因素指数的同度量因素就必须固定在报告期，这样才能保持指数体系在数量上的对等关系。当我们已经确定厂数量指标指数同度量因素固定在基期后，那么质量指标指数的同度量因素就必须固定在报告期。但应注意，虽然我们规定了编制综合指数的两个原则，但在实际编制时，我们要根据研究对象的不同情况、分析任务的不同要求、资料取得方法的难易来具体确定采用何种方法。例如：KP＝∑p1q1/∑p0q1，报告期的ql有时不易得到，所以不得不考虑采用基期的q0，利用KP＝∑p1q0/∑p0q0，故公式的选择在实际中应灵活运用。股票价格指数就是一个实例。(www.daowen.com)

股票价格指数是反映某一股票市场上多种股票价格变动趋势的一种相对数，其计量单位一般用“点（Point）”来表示。即一般将基期指数定为100，每上升或下降一个单位称作上升了一点或下降了一点。股票价格指数的测算方法很多，但一般以发行量为权数采用综合指数的方法进行计算。其计算表达式为

式中：p1i——为第i种样本股票报告期价格；

　　　p0i——为第i种样本股票基期价格；

　　　qi——为第i种股票的发行量，它既可以根据拉氏公式固定在基期，也可以根据派氏公式固定在报告期，但根据综合指数同度量因素确定的原则通常以报告期发行量为权数进行测算。

例7-2 现根据三种股票价格和发行量资料（见表7-4），测算其股票价格指数。

表7-4　三种股票价格和发行量资料

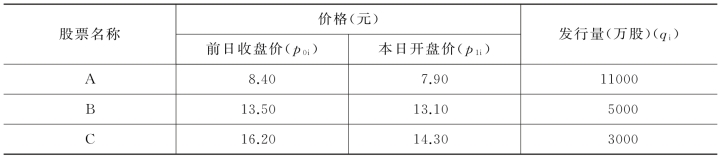
解：根据式（7－5）计算的股票价格指数为

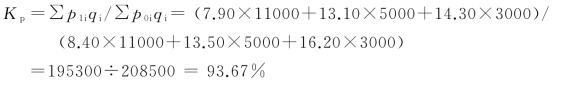
即股票价格下跌了6.33点。