了解了综合指数的定义和特点后，要实际编制综合指数，还必须解决同度量因素固定的时期问题，对于该问题的研究，最具代表性的人物是德国的拉斯贝尔和派许。

1864年，拉斯贝尔提出了同度量因素固定在基期的公式，通常称为拉氏公式：

式中：p（price）——价格；

　　　q（quantity）——物量；

　　　Kp——价格指数；

　　　Kq——物量指数；

　　　∑——总和符号；

　　　下标1——报告期；

　　　下标0——基期。

1874年，派许提出了同度量因素固定在报告期的公式，通常称为派氏公式：

这两类公式为综合指数的建立奠定了理论基础，成为研究综合指数的经典公式，至今仍被广泛应用，同时，由于这两套公式都涉及数量指标指数和质量指标指数，为了便于对比，下面就从数量指标指数和质量指标指数两个角度分别说明拉氏公式与派氏公式的计算原理。

（一）数量指标指数的编制方法

数量指标指数是反映多种现象数量指标综合变化程度的指数。如：产品产量指数、商品销售量指数。

例7-1 某商店经营的三种商品资料如表7-1所示。

表7-1　某商店经营的三种商品综合指数计算表(www.daowen.com)

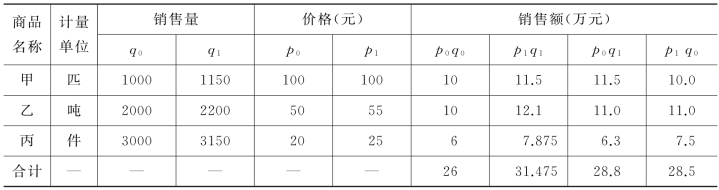
要求：根据上述资料测算该商店的商品销售量指数。

解：根据拉氏公式：

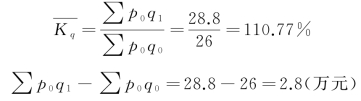
结果表明：从相对数看，在基期价格水平下，三种商品的销售量平均增长了10.77%；从绝对数看，说明纯粹由于销售量的增长使销售额增加了2.8万元。

根据派氏公式：

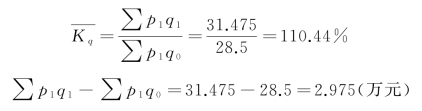
结果表明：从相对数看，在报告期价格水平下，三种商品的销售量平均增长了10.44%；从绝对数看，由于三种商品销售量的上升使销售额增加了2.975万元。

（二）质量指标指数的编制方法

质量指标指数是反映多种现象质量指标综合变化程度的指数。如：成本指数、价格指数。

仍利用【例7-1】资料测算该商店的商品价格指数。

根据拉氏公式：

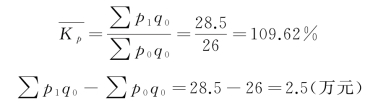
结果表明：从相对数看，在保持基期销售量水平的前提下，三种商品的价格平均上升了9.62%；从绝对数看，由于纯粹的价格上涨使销售额增加了2.5万元，或居民在维持基期生活水准的前提下，由于价格上升，使居民多支出了2.5万元。

根据派氏公式：

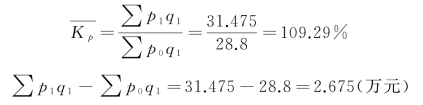
结果表明：从相对数看，在报告期销售量水平的前提下，三种商品的价格平均上升了9.29%。从绝对数看，由于价格上涨使销售额增加了2.675万元，或居民在报告期生活水准的情况下，由于物价上升，需多支出2.675万元。