抽样推断就是用样本的平均数x去推断总体的平均数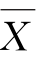；用样本的成数p去推断总体的成数P；用样本的标准差δ去推断总体的标准差σ。要想减少抽样误差，就要求样本具有充分的代表性：①增大样本容量；②抽取的变量接近于总体的平均数；③样本的分布与总体的分布一致。但要判断其代表性，仅从一次试验结果来判断是不可能的，而应该从多次重复试验中，看这种估计量是否在某种意义上来说最接近于被估计的参数真值。这就需要从总体上去考察估计量的优良性，也就是从这些统计量的抽样分布上去考察，通常有三个重要的性质作为选择依据。

（一）无偏性

以抽样指标估计总体指标要求抽样指标值的平均数等于被估计的总体指标值本身。就是说，虽然每一次的抽样指标值和总体指标值之间都可能有误差，但在多次反复的估计中，各个抽样指标值的平均数应该等于所估计的总体指标值本身。即抽样指标的估计，平均说来是没有偏误的。

（二）一致性

以抽样指标估计总体指标要求当样本的单位数充分大时，报样指标也充分地靠近总体指标。就是说，随着样本单位数的无限增大，抽样指标和未知的总体指标之差的绝对值小于任意小的数，它的可能性也趋近于必然性。即(www.daowen.com)

（三）有效性

虽然每个可能样本的抽样指标和未知的全距指标会有离差，但要求抽样指标的标准差比全及指标的标准差更小。或者说，平均来说用样本指标估计相应的总体指标误差都小。

抽样成数是（0，1）分布平均数的表现形式，所以也完全符合优良估计的三项标准。