（一）全距的概念和特点

全距也叫极差，通常用R表示。它是测定标志变动度最简单的方法，计算总体各单位标志值中最大值与最小值之差。他表示总体各单位标志变动度的大小，也反映了总体分散与集中的程度。一般来说，全距大，总体各单位变异程度大；全距小，总体各单位变异程度小。

例4-21 根据【例4-19】资料，计算甲、乙、丙三组学生年龄的全距，并说明标志变动度的大小。

甲组的全距＝24－17＝7（岁）

乙组的全距＝20－20＝0（岁）

丙组的全距＝21－19＝2（岁）

由计算可知，甲组的全距等于7岁，乙组的全距等于0岁，丙组的全距等于2岁，这说明甲组的标志变动度最大，丙组次之，乙组最小。

全距反映总体标志变动度比较直观，且计算简单，但其反映总体标志变动度不是太准确。

（二）平均差的概念和特点

平均差是指各标志值与其算术平均数离差的绝对值的算术平均数。常用A.D表示。其计量单位与标志值的计量单位相同。

由于各个标志值对算术平均数的离差有正有负，其和为零。因此需采用离差的绝对值来计算。平均差仅反映总体各单位的标志值对其平均数的平均离差量。平均差愈大，表明标志变异程度愈大；反之，则表明标志变异程度愈小。用公式表示为

1.对未分组资料，采用简单算术平均式

2.对分组资料，采用加权算术平均式

举例说明平均差的计算：

例4-22 有甲、乙两组工人各10名，他们的平均日产量均为8件，试根据表4-15的资料计算两组工人日产量的平均差，并评价两组工人平均日产量的代表性的大小。

甲组工人日产量平均差：

乙组工人日产量平均差：

由计算结果可知，甲组工人日产量平均差为0.4件，甲组工人日产量平均差为3.6件，乙组大于甲组，由此说明甲组的平均日产量的代表性更大些。

表4-15　平均差计算举例

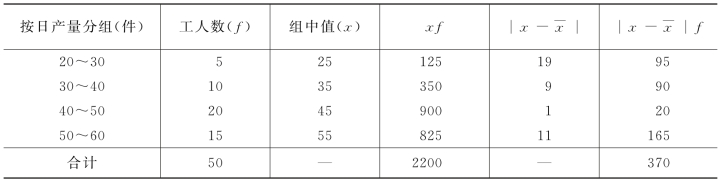
例4-23 根据某生产部门50个工人的日产量资料（表4-16），计算其平均差。

根据表4-16计算：

计算50名工人的平均日产量：

日产量的平均标准差：

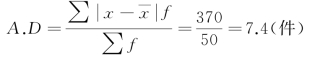
平均差综合了总体各单位的数量差异，因此，能全面地反映总体分布的变异程度。但是，它采用绝对值的方式来消除离差的正负号，不便于代数运算，在数学处理上也不够严密。

表4-16　平均差计算举例

（三）标准差的概念、特点及计算

1.标准差（σ）的概念

所谓标准差就是总体各单位的标志值与其算术平均数离差平方的算术平均数的平方根，故又称为均方根差（简称均方差）。标准差的平方称为方差。标准差的意义与平均差相同，它也是各个标志值对其算术平均数的平均离差。但在数学处理上与平均差有所不同，它是采用平方的方法来消除离差的正负号的，因此它比平均差更能准确地反映变量数列之间的离中程度，是统计中最常用的标志变异度指标。

2.标准差的计算步骤和方法

根据标准差的定义，标准差的计算步骤为：

第一，求总体各标志值的算术平均数；第二，求总体各标志值与其算术平均数的离差；第三，求离差的平方；第四，求各项离差平方的算术平均数；第五，对离差平方的算术平均数开平方。

根据所掌握的资料不同，标准差的计算可分为简单平均法与加权平均法两种。

（1）简单平均法

在资料未分组的情况下：

（2）加权平均法

在资料分组的情况下：

例4-24 某车间甲、乙两个生产小组日产量资料如表4-17所示，试求标准差。

表4-17　标准差计算举例

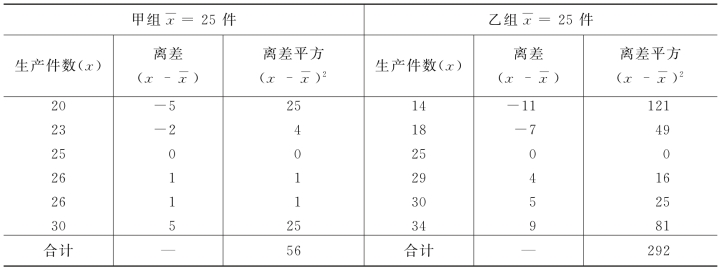
根据表中资料计算

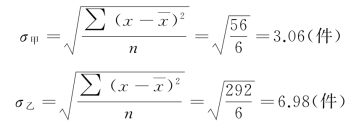
通过计算可知：甲组的标准差小于乙组，其标志变异程度也就小于乙组，因此甲组的平均数比乙组更有代表性。

例4-25 以表4-16资料计算标准差，如表4-18所示。

表4-18　标准差计算举例

注：x＝44（件）.

根据上表资料计算得(www.daowen.com)

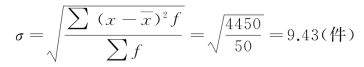
计算结果表明，标准差愈大，标志变动程度越大；标准差愈小，标志变动程度越小。

3.标准差的数学性质与简捷计算

（1）标准差的数学性质

标准差的平方σ2称为方差，方差具有如下性质：

第一，各变量值x与其算术平均数x计算的方差小于各变量值x与任意数A计算的方差。即

式中：A——任意数。

这一性质还可表述为标志值对其算术平均数的标准差为最小。

第二，变量的方差等于变量平方的平均数减变量平均数的平方。即

利用这一性质，可以进行标准差的简捷计算。

（2）标准差的简捷计算

根据标准差的性质，我们可以得出标准差的简捷计算公式：

在资料未分组的情况下：

在资料已分组，且为单项式资料的情况下：

在资料已分组，且为等距式资料的情况下：

式中：A——接近于平均数的常数；

　　　Δ——等距数列的组距。

例4-26 以某乡粮食生产资料为例，按简捷法计算标准差，见表4-19。

表4-19　简捷法计算标准差

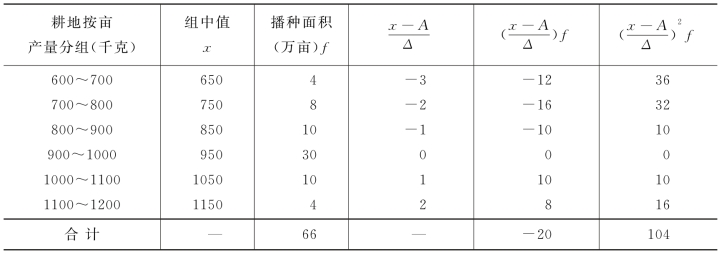
注：A＝950；Δ＝100.

将表中的数字代入公式得

对于等距数列来说，用简捷法比普通法要简便得多。

4.是非标志标准差

所谓是非标志（又称交替标志），是指仅有两种标志表现的品质标志。例如，产品的合格与不合格；人口的男性与女性等，这种用“是”与“非”或“有”与“无”来表示的标志要测定这类标志的变动程度，也需要计算标准差，其原理与前述的内容一致，但在计算形式上有区别。所以应首先将是非标志的具体表现数量化。即将所研究现象标志表现（x）分别用“1”和“0”来表示，然后计算其平均数和标准差。

设全部总体单位数为N，具有某种性质的单位数为N1，其比重为P；不具有某种性质的单位数为N0，其比重为Q。则

具有某种性质的单位数的比重：

不具有某种性质的单位数的比重：

所以，P＋Q＝1

那么，是非标志的算术平均数及标准差计算如表4-20所示。

表4-20　是非标志的算术平均数及标准差计算表

可推出：

是非标志的算术平均数

是非标志的标准差

例4-27 某企业产品合格率为95%，不合格率为5%，则

关于是非标志的平均数和标准差在“抽样组织与假设检验”中常用，且当p＝50%时，其标准差取最大值0.25。对确定最少抽样数目有很大的帮助。

（四）变异系数的意义和计算

以上所介绍的变异度指标，都是有计量单位的名数。它们是从绝对量上反映数列的变异程度，其数值的大小除了受总体内部标志值的差异程度影响外，还受标志本身水平高低的影响，若直接用上面指标比较不同水平数列的变异程度显然不合适，因而需要消除平均水平高低的影响，消除的办法就是用标准差指标与其自身的算术平均数对比，计算标准差系数Vσ，也叫变异系数。这是实际工作中最常用的一个统计指标。现仅以标准差为例，介绍变异系数的计算。其计算公式为

例4-28 有两个工厂工人劳动生产率资料如表4-21所示，试确定哪一个工厂的劳动生产率更有代表性。

表4-21　标准差系数比较表

要比较哪一个工厂的劳动生产率更具有代表性，直接用标准差对比不合理，因为两个工厂劳动生产率水平相差悬殊，需要进一步计算标准差系数。

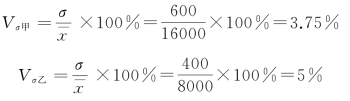
甲厂的标准差系数小于乙厂，说明甲厂的劳动生产率更有代表性。