（一）中位数的概念

中位数（Me）是指位于总体分布中点位置上的标志值。所谓分布中点，意味着有一半单位的标志值小于该点的标志值，而另—半单位的标志值必定大于该点的标志值。由此可见，中位数的大小不受两端值的影响，也不受各变量变动大小的影响，仅受所处位置的影响。由于许多事物的分布均呈正态分布或近似正态分布，因此中位数可以从另一侧面反映次数分布的集中趋势。

（二）中位数的确定方法

1.根据未分组资料确定中位数

对于未分组的资料x1，x2，…，xn进行排序后，按下列公式确定众位数的位置。

式中，n代表数列的项数。

如果项数是奇数，则居于中间位置的那个变量值就是中位数。

例4-15 有5位学生的年龄按顺序排列为15、18、19、20、23，求中位数。

中位数位置＝＝3表明中位数在第3项位置上，则

中为数Me＝19（岁）

如果项数是偶数，则中间位置的两个变量值的算术平均数就是中位数。

例4-16 有6位学生的年龄按顺序排列为15、18、19、20、21、23，求中位数。

2.根据分组资料确定中位数

分组资料可以分为单项式变量数列和组距式变量数列。

（1）对于单项式变量数列。

首先，要确定中位点∑f/2所在的组，即累计次数的半值；

其次，找出中位数所在的组，即含累计次数半值的组，该组的变量值就是中位数。

例4-17 某生产车间120名工人生产某种零件的日产量分组资料如表4-12所示，确定该车间工人日产量的中位数。

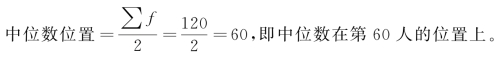
根据计算的累计次数资料可知，累计次数∑f中含有60的累计次数为77（向上累计）或73（向下累计），该组即为中位数组，由此可以确定中位数为26件。

表4-12　某生产车间工人日产量分组资料

(www.daowen.com)

（2）对于组距式变量数列。

由组距数列确定中位数，同样要先按中位点的公式确定中位数所在的组，然后按照下限公式或上限公式来计算中位数的近似值。

中位数的下限公式：

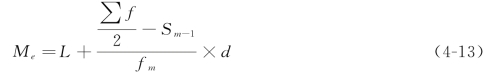
中位数的上限公式：

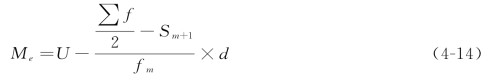
式中：L——中位数所在组的下限；

　　　Sm－1——中位数所在组前一组的累计次数（其累计次数按向上累计计算）；

　　　fm——中位数所在组的次数；

　　　d——中位数所在组的组距；

　　　U——中位数所在组的上限；

　　　Sm＋1——中位数组后一组的累计次数（累计次数按向下累计计算）。

例4-18 某市2019年对某企业职工月收入进行抽样调查，资料如表4-13所示，试确定职工收入的中位数。

表4-13　某市2019年工业企业职工月收入抽样调查资料

据表4-13资料计算：

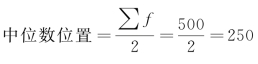
即中位数应使这个数列中各有250名工人的工资在其上下。根据计算出的累计次数资料可知，中位数位于第四组，则11000～14000组就是中位数所在的组。

根据下限公式计算中位数：

根据上限公式计算中位数：

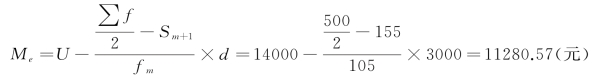
可见，不论是按照下限公式还是上限公式，同一资料所计算的中位数是完全相同的。