（一）调和平均数的概念

调和平均指标也叫调和平均数，是根据标志值的倒数计算的，它是标志值倒数的算术平均数的倒数，所以亦称为倒数平均数，用来表示。在统计实践中，由于只有各组标志总量和各组变量值，而缺乏总体单位数资料，不能直接采用算术平均数计算，这时就需要将算术平均数的形式加以改变，按照算术平均数基本算式的需要，算出所需总体单位数，继而再计算平均数，这样就得到另一种平均数的计算方法，这就是调和平均数。调和平均数分为简单调和平均数和加权调和平均数两种。

（二）简单调和平均数

简单调和平均数方法适用于未分组资料或资料虽分组，但各组标志总量均相等的情况。下面结合实例加以说明：

例4-7 设市场上某种蔬菜早市每千克0.50元，中午每千克0.40元，晚市每千克0.25元，若早、中、晚各买1元，问平均每千克的价格？

以下我们从几个方面加以分析：

（1）早、中、晚各买1元，共买了3元；

式中：xH——调和平均数；

　　　x——各标志值；

　　　n——变量值的个数。

（三）加权调和平均数

加权调和平均数方法适用于资料已分组，且各组标志总量不相等的情况。其计算公式为

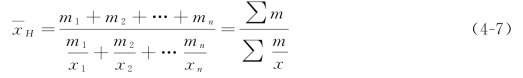
式中，m代表各组标志总量。

例4-8 上例中，早、中、晚各买1元钱的蔬菜，现在假设早、中、晚各购买4元、5元、6元，求平均价格，如表4-6所示。

表4-6　加权调和平均数的计算

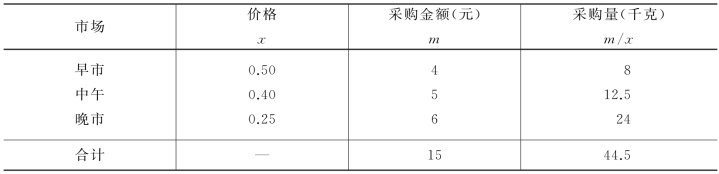
平均价格为(www.daowen.com)

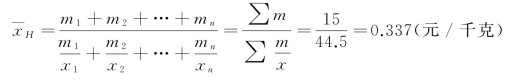
（四）加权调和平均数与加权算术平均数的关系

从形式上说，加权算术平均数与调和算术平均数的原式存在两点区别：一是算术平均数以x为变量，调和平均数则以1/x为变量；二是算术平均数的权数是f，代表次数单位数，而调和平均数的权数却是xf，代表标志总量。但两者实质上都是标志总量与总体单位数之比。调和平均数可以称为算术平均数的变形。

在对算术平均数与调和平均数的介绍当中，我们可以发现这样的特点：在计算平均指标时，若缺少分子资料时，既缺少总体的标志总量，则适宜采用加权算术平均数；若缺少分母资料时，既缺少总体的单位总量，则适宜采用加权调和平均数的方法。现举例说明。

例4-9 某公司所属3个工厂2019年的产值完成情况及计划产值资料如表4-7所示。

表4-7　3个工厂完成情况及计划产值

则3个工厂平均计划完成程度为

例4-10 假如【例4-9】中已知的是该公司所属3个工厂2019年的产值完成情况及实际产值资料（如表4-8所示），计算3个工厂平均计划完成程度。

表4-8　3个工厂完成情况及实际产值

则3个工厂平均计划完成程度为

（五）运用调和平均数应注意的问题

（1）当变量数列有一变量x为零时，调和平均数公式的分母将等于无穷大，因而无法求出一确定的平均值。

（2）调和平均数与算术平均数一样，易受极端变量值的影响，当数列存在极端大的数值时，调和平均数增大；当数列存在极端小的数值时，调和平均数减小。

（3）要注意调和平均数和算术平均数的使用条件，因事制宜。