（一）算术平均指标的基本形式

算术平均指标是统计中最基本、最常用的一种综合指标。它是将总体各单位的标志值相加求其算术总和，然后除以总体单位个数而得。其基本公式为

在社会经济现象中，有许多被研究总体，其各单位标志值的总和常常形成一个具有独立经济范畴的总量指标，即标志总量，如各个职工的工资总和，形成工资总额，各单位面积收获量的总和，形成总收获量。而算术平均数的计算方法与社会经济现象的这种特点相适应，即总体的标志总量等于总体各单位某一数量标志值的算术总和，所以，算术平均数的得以广泛应用。

利用公式（4-1）计算平均数时应注意：（1）公式的分子和分母存在着密切的关系，其分子（标志总量）是由分母中总体单位本身所具有的某种标志值加总而得到的。这是平均指标与强度相对指标最本质的区别。（2）总体标志总量是数量标志值之和，由于品质标志不能相加，因而不能计算算术平均数。（3）算术平均数是一个有名数，计量单位和标志值的计量单位一致。

若具备总体标志总量与总体单位总量时，可直接利用上面的公式计算，在不具备上述条件时，可根据具体情况而定，通常可采用简单算术平均数和加权算术平均数两种形式计算。

（二）算术平均数与强度相对数的区别

在实际社会经济生活中，某些强度相对指标会被误认为平均指标，如“人均汽车占有量”“人均手机持有量”等，虽然这类指标有“人均”二字，有“平均”的含义，但它们不是平均指标，而是强度相对指标，必须弄清二者的区别。算术平均数与强度相对数的区别主要表现在以下两点：（1）分子、分母资料是否属于同一总体范围。平均指标的分母、分子是同一总体的单位总量和某一标志总量，且分子直接依附于分母；强度相对数的分子与分母本质上分别属于两种性质不同但有联系的现象总体；（2）分子与分母数值是否具有一一对应关系。平均指标中分子的标志总量就是分母的单位总量中每一单位的标志值之和，且各个标志值与各个单位一一对应。

（三）简单算术平均数

在计算算术平均数时，若掌握的资料是总体各单位的标志值，那么就可以将总体各单位的标志值简单相加求得标志总量，然后除以总体单位总量，即得平均数。这种方法通常称为简单算术平均法。用公式表示：

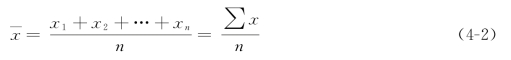
式中，x代表算术平均数；x代表各单位标志值；n代表总体单位数；∑x为求和符号。

例4-1 某生产小组有12名工人，每个工人日产某种产品件数为：17，15，18，16，17，16，14，17，16，15，18，16，则该班组平均工人日产量为

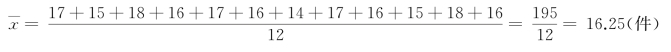
（四）加权算术平均数

加权算术平均数一般用来计算分组资料的算术平均数，它是用标志值乘以相应的各组单位数求出各组的标志总量，并加总求得总体标志总量，再除以总体单位总数即得。

设有n个标志值x1，x2，…，xn，如果以f1，f2，…，fn为各标志值的权数或次数，则x的加权算术平均数计算公式为。

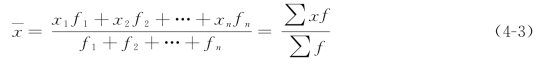
式中，x代表各组标志值；f代表各组单位数。

计算加权算术平均数时有两种情况：一是单项式变量数列计算；二是组距式数列计算。

（1）根据单项式变量数列计算算术平均数。由单项式变量数列计算算术平均数，是将各组的标志值乘以相应的各组的单位数，求出各组标志总量，并加总得出总体的标志总量，同时把各组单位数相加求出总体单位总数，然后，再用总体单位总数去除总体标志总量，即得算术平均数。

例4-2 某车间有工人120人，将他们每人每日生产某种零件数编制成单项数列如表4-1所示。

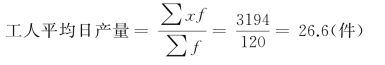
从以上的例题中，我们可以看到，加权算术平均数同时受到标志值x与权数f的共同影响。其中权数起着权衡标志值对平均数影响程度的作用。一般来说，在分组资料中，标志值小的组拥有较多的次数时，平均数倾向于标志值小的一方；当标志值大的组拥有较多的次数时，平均数倾向于标志值大的一方。这里次数f起着权衡轻重的作用，因此统计中常称它为“权数”，加权算术平均数也由此而得名。

表4-1　加权算术平均数计算

这里需要说明的是，如果各组次数（权数）完全相等，即f1＝f2＝…＝fn，则各组次数对平均数的影响就会相同，从而它不再起权衡轻重的作用。这时加权算术平均数就等于简单算术平均数。

权数可用绝对数来表示，也可用各组单位数占总体单位数的比重来表示，即权重系数。权重系数亦称为频率，是一种结构相对数。用频率为权数的加权算术平均数等于各组变量值乘以相应的频率之和。即

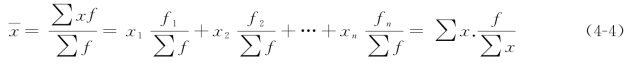
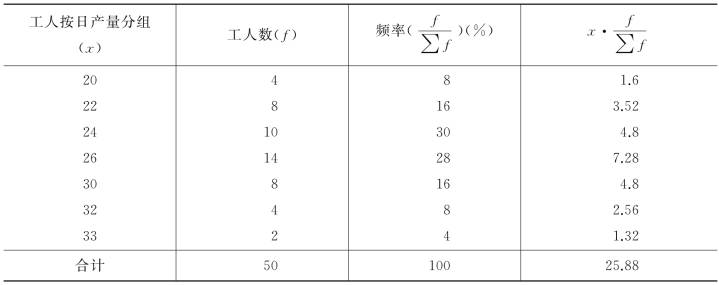
例4-3 某车间有工人50人，将他们每人每日生产的某种零件数编制成单项式数列，如表4-2所示。

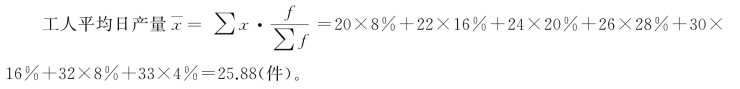(www.daowen.com)

由计算结果可以看出，比重的大小直接表明了该组标志值占据平均数的地位。比重的数字意味着：日产零件20的工人中，有8%计入了平均数，日产零件22的工人中，有16%计入了平均数，每组工人所占工人总数的比重越大，该标志值占平均数的地位就越大。由此可见，在分组资料中，标志值小的组拥有较大的比重时，平均数倾向于标志值小的一方；当标志值大的组拥有较大的比重时，平均数倾向于标志值大的一方。

表4-2　某车间工人按日产量分组的各组工人频率分布表

（2）根据组距式变量数列计算算术平均数。如果掌握的是组距数列资料，其计算方法与上述方法基本相同，有一点不同的是，组距数列以各组的组中值作为变量值。利用组中值计算平均数有一定的假定性，首先假定各个组的标志值在组内的分布是均匀的，但实际上各组内的标志值分布不会绝对均匀。其次如果组距数列上下两组是开口组，还假定他们与同临组组距相仿，这与实际也有出入，所以根据组距数列计算出的加权算术平均数只是近似值。

例4-4 某工业局所属的生产同一产品的企业按工人劳动率高低分组的资料如表4-3所示，计算平均劳动生产率。

表4-3　某工业局所属企业的劳动生产率情况表

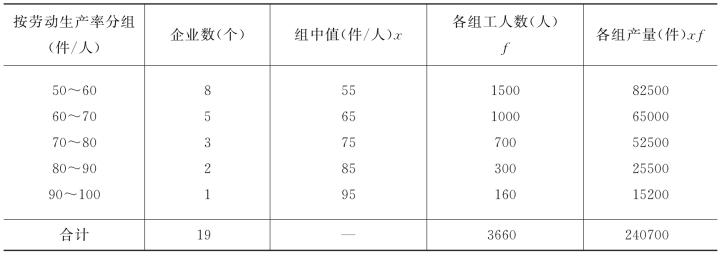
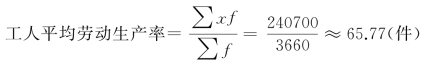
在组距数列中没有具体的标志值，各组的组限只表明标志值的上下界限，因此必须先算出各组的组中值来代表各组的标志值，然后计算加权算术平均数。

计算加权算术平均数会遇到权数的选择问题。一般来说，在分配数列条件下，次数常常就是权数，但也有例外的情况，如上例中，企业数虽然是劳动生产率不同的各组的次数，但不是合适的权数，不宜用它来进行加权计算。通常权数的选择应该同时满足两个条件：其一，它必须是标志的直接承担者；其二，它与标志值相乘所得的标志总量应是一个真实反映实际，并具有经济意义和社会经济内容的总量指标。

（五）算术平均数的数学性质和应用

1.算术平均数的数学性质

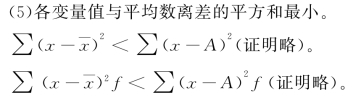
2.算术平均数的简便运算

在计算算术平均数时，有时由于被平均的标志值较大，计算烦琐，有必要采用简捷法计算。其基本的思路是：通过变量值的线性变换，将原变量数列的标志值简化，由此简化算术平均数的计算过程。

根据数学性质（2），可把原来较大的数值变为简单的数据运算，所得结果再变换为数据的平均数。

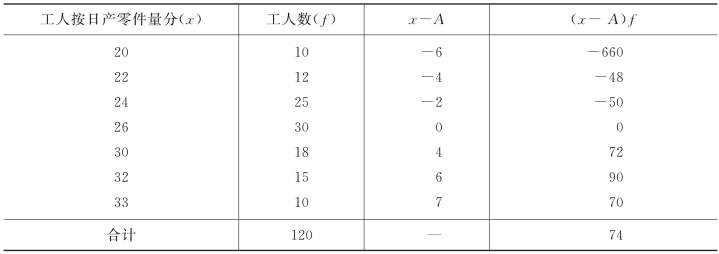
例4-5 某车间有工人120人，将他们每人每日生产某种零件数编制成单项数列如表4-4表示。用简便法计算平均日产量。

表4-4　算术平均数的简捷计算法

该车间工人平均日产量为

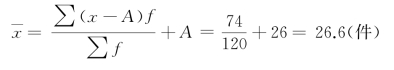
以上数学性质也可以综合运用，使计算过程更加简化。根据数学性质（2）、（3），推导出算术平均数的简算公式：

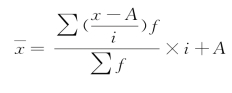
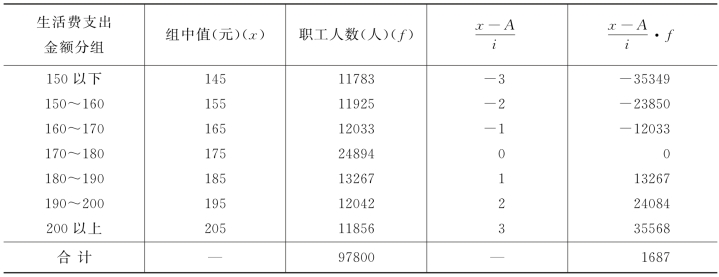
例4-6 某市职工生活费支出和人数如表4-5所示，计算该市职工平均生活费支出。该市职工平均生活费支出：

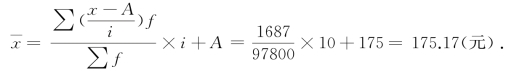
表4-5　算术平均数的简捷计算法 （A＝175、i＝10）

（六）简单算术平均数与加权算术平均数的关系

简单算术平均数与加权算术平均数均为计算算术平均数的基本形式，二者的区别：一是二者掌握总体单位资料的详尽程度不同，如果掌握了每一个总体单位的标志值，计算平均数时，用简单算术平均数；如果掌握了总体单位分组的标志值及各组的单位数，计算平均数时，用加权算术平均数；二是二者的计算精确程度不同，简单算术平均数，计算的平均数是精确值，而加权算术平均数，计算的平均数是近似值。二者的联系是：当各组的权数相同时，加权算术平均数就变成了简单算术平均数。