就分配数列而言，品质数列和单项数列都很容易编制。品质数列一般分组标志确定了，则分组单位数也就随之确定了。单项数列由于它应用的条件是变量值项数较少，变动幅度小，故较易编制。而当变量值的项数较多，变动幅度较大时，就需要编制组距数列。下面结合具体实例说明组距数列的编制方法。

例3-1 某百货公司50天商品销售额（单位：万元）数据资料如下：

36 38 35 43 35 38 32 28 46 43

44 42 32 45 34 33 39 46 36 38

44 49 34 37 47 43 37 30 37 35

48 45 43 45 29 40 37 37 36 25

42 36 44 46 40 30 42 26 42 41

要求：编制组距数列并说明数据的分布特征。

从资料可以看出，数据较多，若编制单项数列，则不便于观察数据的分布特征及变动规律，因此，应当采用组距分组，编制组距数列。其步骤为下面几步。

（一）确定全距

全距是总体中某一数量标志的最大值与最小值之差，用符号R表示。即

对于此例，R＝49－25＝24

确定全距是为了确保在编制变量数列时，总体中的每一个单位都有一个组可以分配而不被遗留。

（二）确定组数

组数即分组的个数。确定组数需要考虑的因素很多，其中最根本的原则就是要体现出各组间质的不同，此外还要考虑总体单位数的多寡、全距的大小，但最通用的一般方法是借助于美国学者斯特吉斯的经验公式作为确定组数时参考。他认为：当总体单位按某标志分组接近正态分布时，可根据总体单位数N确定组数k。

其公式为

在此，我们不妨采用斯特吉斯的经验公式来确定组数，即k＝1＋3.322lg50＝6.6，取组数为整数7。

（三）确定组距

组距是指各组中最大值与最小值之差，用i表示。确定组距需要考虑的因素也很多，其中最根本的原则就是要体现出各组内的同质性，此外还要考虑研究目的要求、数列分布的偏斜程度等，但最通用的一般方法仍是在美国学者斯特吉斯提出的经验公式基础上进行测算。由于在一数列有

关系成立，故有

对于本例i＝24/7＝3.429，调整为整数4，有时为了方便起见，组距i一般只取5或10的整数倍，即还可以调整为5。但无论怎样确定都要满足i×k≥R这一条件。在此，不妨先选取组距为4，以使得实际选用的组距更接近于理论组距。

（四）确定组限

组限是组距两端的分界限。组限的合理确定至少要考虑以下几个因素。

1.根据变量的性质确定重叠组限与不重叠组限

所谓重叠组限即指相邻两组用同一数字界开，它适用于连续型变量，其目的是为了避免漏值。因为连续型变量两数之间可做无限分割，不能一一列举。如按月收入分组：2000元以下、2000～4000元、4000元以上。重叠组限对于越大越好的变量（一般称之为“正指标”），通常按“上限不包括在内”的原则归组。如上例的2000元应归入2000～4000元这一组。而对于越小越好的变量（一般称之为“逆指标”），通常按“下限不包括在内”的原则归组。例如，产品单位成本计划完成百分比的分组为80%～90%、90%～100%、100%～110%。其中，100%应归入90%～100%这一组。

不重叠组限是指相邻两组用顺序的整数界开，它适用于离散型变量。例如，按人数分组为500人以下、501～1000人、1001人以上。但在实际中，为方便起见，离散型变量也可以采用重叠组限。对于此例来讲，由于销售额为连续型变量，故必须采用重叠组限。(www.daowen.com)

2.根据极端值的存在与否确定首、末组是采用开口组还是闭口组

闭口组即指上、下限齐全的组。如，“50～60分、60～70分、70～80分、80～90分、90～100分”这一学生成绩的分组。开口组即指最小组下限或最大组上限不能完全确定，往往标有“××以上”“××以下”的字样。

如果数据分布较集中，不存在极端值，则首末组适宜采用闭口组；如果数据分布较分散，并且存在着极端值，则首末组适宜采用开口组。

对于开口组，有时由于计算的需要，还要将其所缺的上限、下限补齐，其处理方法是若数列按从小到大排列，则开口组假定组限的确定公式为

若学生学习成绩分组为：“60分以下、60～70分、70～80分、80～90分、90分以上。”

则首组的假定下限＝60－10＝50（分）

末组的假定上限＝90＋10＝100（分）

但这种方法有时也会出现问题。

例如，西瓜按重量分为三组：“2千克以下、2～6千克、6千克以上”

末组的假定上限＝6＋4＝10（千克）

首组的假定下限＝2－4＝－2（千克），出现负值，这与事实不符。应将－2改成0，因为西瓜至少是不存在，但不可能为负数。一般地，当计算出的假定上限、下限超越实际可能的极限时，应当将其固定在极限值上。

对于此例，由于不存在极端值，因此首末组不必采用开口组，而应采用闭口组。

3.根据能否反映数据的真实分布特征确定初始值

初始值的确定有两种基本方法：其一是以小于或等于最小变量值作为第一组的下限，其二是以最小变量值作为第一组的组中值。但都要满足组距数列中的“首组的下限（初始值）≤数列中的最小值”“末组的上限数列中的最大值”两个条件。一般地，可同时做出几种结果并从中选出最能反映数据的真实分布特征的初始值。对于【例3-1】，不妨选取数列中的最小变量值作为第一组的下限，则组限确定的情形为：“25万～29万元、29万～33万元、33万～37万元、37万～41万元、41万～45万元、45万～49万元、49万～53万元”。

（五）分配各组次数

在归组时，为了“不重不漏”，由于商品销售额为越大越好的变量（“正指标”），故遵循“上限不包括在内”的原则归组，同时计算出各组的频数与频率。其结果如表3-7所示。

表3-7　某百货公司商品销售额分布状态

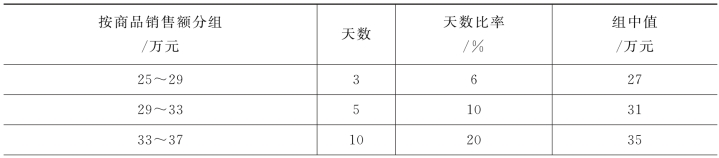
续表

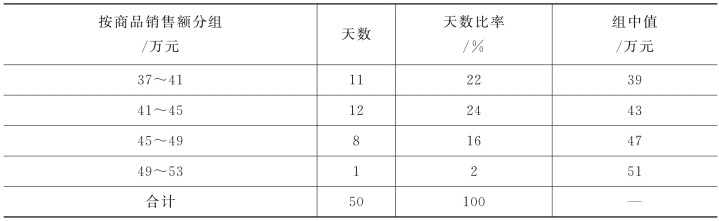
（六）计算组中值

组中值即指各组上限与下限之间的中点数值、其计算公式为

为什么要计算组中值呢？因为组距数列掩盖了各组内的数据分布状况。为了反映各组中数据的一般水平，往往用组中值来代表。其假定前提条件是：各单位的变量值在本组范围内呈均匀分布，即：比组中值大的和比组中值小的一样多，大小数值相抵后刚好等于组中值。完全具备此条件是不太可能的，但应尽可能地满足这一要求，以减少用组中值代表各组变量值一般水平时所造成的误差。

对于开口组，首先要确定假定上、下限，然后，再利用该公式求得。

或者利用下列公式求得

经过上述六个步骤，一个完整的组距数列就形成了，由此可以看出该百货公司50天商品销售额的分布呈“两头小、中间大”的钟型分布状态，这也是统计分布的一种常态。