根据Nakajima（2011）的研究，我们首先给出以下变量的先验分布：，同时给出各相关变量的初始值：。

给定以上的先验分布和初始值后，我们首先预烧样本1000次，以纠正初始赋值对后验分布估计结果的影响。然后运用蒙特卡洛模拟方法（MCMC）连续抽样10000次进行迭代模拟，最终获得各参数的后验分布情况。为了确定最佳的滞后期，我们测算出了模型滞后期阶数的边际似然估计值，一般而言估计值越小模型的拟合度越高，最终我们选定滞后期为1期。同时考虑到不同模型设定带来的偏误，我们对包含有截距项和不包含有截距项的模型都进行了回归。回归结果如表7-3所示。

表7-3　不带截距项的参数回归结果

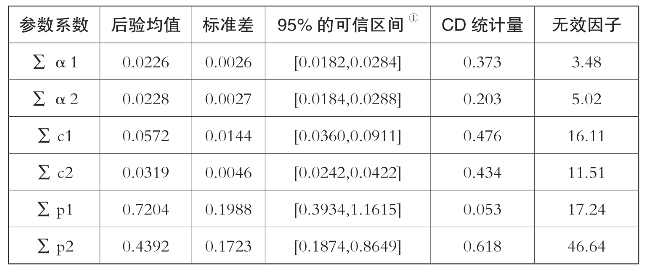
① 与常规参数“置信区间”的表述不同，对于不确定性参数，我们使用了可信区间的概念。

其中，CD（convergence diagnostics）统计量是Geweke（1992）提出的检验统计量，主要检验模型马尔科夫链的收敛情况，该统计量的原假设是参数估计的后验分布收敛，备择假设是参数估计的后验分布发散；无效因子主要是用来评估蒙特卡洛模拟链总体的自相关程度。

表7-4　带截距项的参数回归结果(www.daowen.com)

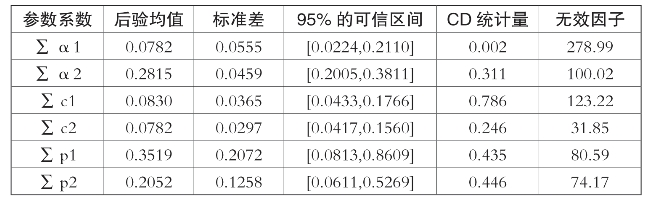
注：CD和无效因子的解释如上。

对比表7-3和表7-4可知，带有截距项模型的无效因子统计量远大于不带有截距项模型的无效因子，这表明带有截距项的参数估计模型不够稳定。因此本书选定不带截距项的参数估计模型。根据不带截距项的参数估计结果可知，在95%的可信区间内，CD统计量和无效因子检验结果均表明估计结果是收敛的，并且非常稳健，说明运用MCMC方法很好地实现了对待估参数后验分布的估计。即使是无效因子较高的∑p2，我们也获得了至少M/50=200个不相关的样本，这对于后验分布估计也已经足够了。

为了进一步分析抽样结果的稳健性，我们可以通过抽样自相关估计图、抽样路径图和后验分布密度图来直观的观察抽样状况。

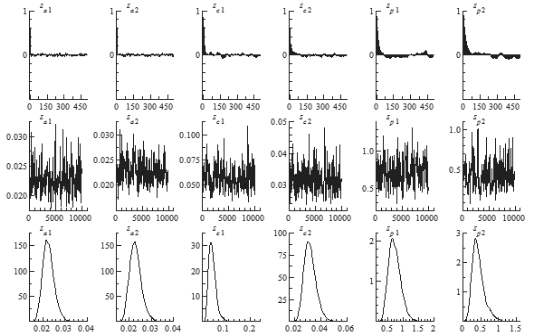
图7-4　运用随机波动模拟数据获得的模型估计结果

图7-4中，第一行代表了抽样自相关估计结果图，第二行代表了抽样路径图，第三行代表了后验分布的密度图。从自相关估计图上可以看出，抽样样本的自相关系数迅速收敛于0，没有出现明显的发散现象，抽样结果是非常稳健的。从抽样路径图上，抽样数据呈现明显的波动集聚现象，在随机扰动下围绕后验估计值进行随机波动，估计结果是有效的。后验分布密度图可以发现，数据主要集中分布于待估参数区间内，估计结果有效。