（一）模型稳定性检验和最优滞后期

建立VAR模型首先要满足平稳性的假定，平稳性要求通用特征方程的特征根均要位于单位圆以内，稳定性检验结果如图6-3、图6-4所示。

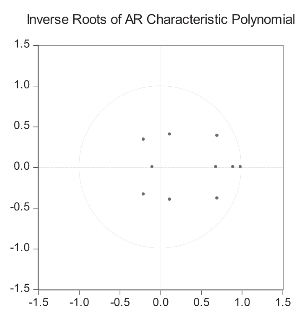
图6-3　原变量稳定性检验

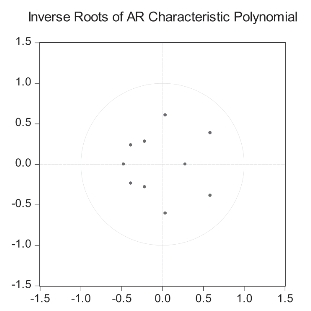
图6-4　一阶差分后稳定性检验

由稳定性检验可知原变量的单位根有一个位于单位圆之外，var模型不满足稳定性的要求。差分后的特征根均位于单位圆内，表明差分后的模型满足稳定性要求，可以进行脉冲响应、方差分解等后续的计算和分析。

建立VAR模型除了要满足平稳性条件外，还应该确定滞后期k值。如果滞后期太少，误差项的自相关会很严重，并导致参数的非一致性估计。但从另一方面看，k值又不宜过大，k值过大会导致自由度减小，直接影响模型参数估计量的有效性。本书采用了LR、FPE、AIC、SC、HQ等多种方法对最优滞后期进行了检验，检验结果如表6-4所示。

表6-4　var模型滞后期检验结果

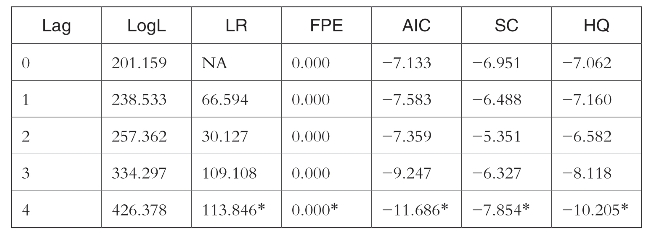
注：*表示按规则所选择的滞后期；显著性水平为5%；LR：sequential modified LR test statistic；FPE：Final prediction error；AIC：Akaike information criterion；SC：Schwarz information criterion；HQ：Hannan-Quinn information criterion

综合不同的信息准则检验结论，本书最终确定模型的最优滞后期为4期。

（二）协整检验

在进行时间系列分析时，传统上要求所用的时间序列必须是平稳的，即没有随机趋势或确定趋势，否则会产生“伪回归”问题。但是在现实中，宏观经济数据一般来讲是不平稳的。面对这个问题，有两种解决方法：一种是对非平稳变量进行差分，由于差分后的数据可以剔除趋势性因素，因此往往可以满足数据平稳的要求，可以进行后续的回归分析。但是差分也让我们失去了关于变量之间长期关系的信息，并且很多时候这种长期信息对于研究变量之间关系至关重要。另外一种方法就是运用协整的方法，这种方法可以不在损失数据信息的情况下，考察非平稳变量之间的长期均衡关系。在进行协整分析之前首先要确定两组非平稳变量之间是否存在协整关系，也即存在非平稳变量之间的长期均衡关系。协整检验的方法有很多，最典型的就是Engle-Granger检验和Johansen检验，其中Engle-Granger检验只能用于检验两个变量之间的协整关系，Johansen检验不仅在检验变量上没有这种限制，而且可以同时求出变量之间的协整关系。因此，本书在进行协整检验时采用Johansen检验方法。

协整检验主要是判断协整关系的个数，检验公式如下所示：(www.daowen.com)

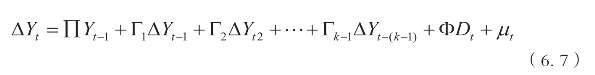
其中Y表示非平稳变量，Π、Γ、Φ表示系数，D表示截距项，u表示随机扰动项。如果检验存在r个协整向量，即（N-r）个非协整向量或者（N-r）个单位根，可以表达为相应的（N-r）个特征值。协整个数的检验主要有两种方法：迹检验和最大特征值检验，为了保证检验结果的稳健性和一致性，本书运用了两种检验方法，检验结果如表6-5、表6-6所示。

表6-5　协整向量个数r迹统计量检验

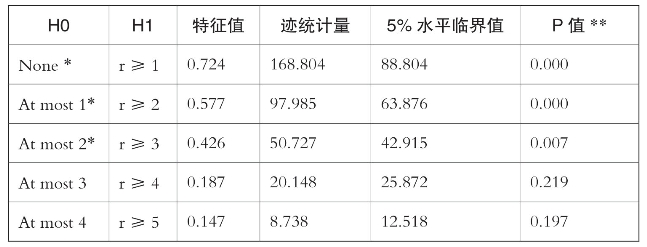
注：*表示在5%的显著性水平下拒绝原假设；
**表示MacKinnon-Haug-Michelis（1999）的p值。

表6-6　协整向量个数r最大特征值检验

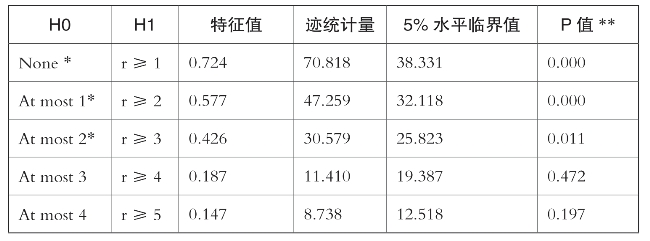
注：*表示在5%的显著性水平下拒绝原假设；
**表示MacKinnon-Haug-Michelis（1999）的p值。

迹统计量检验表明：因为50.727＞42.915，所以拒绝原假设“At most 1（存在一个协整关系）”，同时20.148＜25.872，接受原假设“at most 2（存在两个协整关系）”；最大特征值检验表明：因为30.579＞25.823，所以拒绝原假设“At most 1（存在一个协整关系）”，同时11.410＜19.387，接受原假设“at most 2（存在两个协整关系）”。迹统计量和最大特征值检验均表明，政策透明度（mpt）、经济增长（pcg）、历史通胀水平（pil）、金融深化（tfd）和经济开放度（eti）之间存在两个协整关系。

（三）向量误差修正模型（VECM）

根据格兰杰定理，如果若干个非平稳变量之间存在协整关系，则必然存在误差修正模型。误差修正模型可以在不损失变量信息的情况下对变量长期均衡关系进行量化分析。向量误差修正模型（VECM）是在解释变量中含有协整约束的VAR模型，它适用于分析已知有协整关系的非平稳序列之间的关系。根据协整向量个数检验结果表明mpt、pcg、pil、tfd和eti之间存在两个协整关系，因此进入VECM模型的误差修正项分别是：

（四）求扰动相关系数矩阵

通过对一阶差分变量的误差修正模型（VECM）估计，我们可以得到扰动项的无条件相关系数矩阵。