本章中主要是基于结构化向量自回归模型（SVAR）和有向无环图（DAG）进行分析，下面将会简要介绍这两个模型。

（一）结构化向量自回归模型（SVAR）

自Sims（1980）提出向量自回归模型（简称VAR模型）后，因为其在参数回归方面具有的优势，所以被广泛运用于计量分析中。但是该模型也存在很多问题，如模型的建立不以经济理论为基础，不分析回归参数的经济意义；对参数不施加零约束，模型待估参数过多；模型不包含任何当期变量，不能考察变量当期之间的关系等。基于此，Blanchard和Perotti（1999）提出了一种结构化的向量自回归模型（structural vector auto regression model），简称SVAR模型。该模型基于一定的经济理论，将经济理论中变量之间的结构性关系引入标准的VAR模型中，即在VAR模型中加入具有单向因果关系的内生变量当期值。SVAR模型可以体现出变量之间当期的结构性关系，并且对待估参数进行了结构化约束，很好地解决了标准VAR模型存在的一些问题。

若令滞后阶数为k，变量个数为n，则VAR模型的一般形式可用下式表示：

其中，Yt表示由第t期观测值构成的n维列向量，Ct表示由截距项构成的n维列向量，Π为n*n系数矩阵，v是由随机误差项构成的n维列向量，并且随机误差项vt（t=1，2，…n）为白噪声过程。

在标准VAR模型中加入具有因果关系的当期变量就变成了SVAR模型，模型如下所示：

估计SVAR模型需要对模型的结构式A和B做施加约束，一般而言，对于n元P阶的结构化模型需要对结构式施加[n（n-1）]/2个约束条件，才能识别出结构冲击（刘金全，2000）。对扰动项的结构式进行正确的设定是后续运用SVAR模型进行方差分解和脉冲响应等分析的基础，因此非常重要。目前研究中对结构化模型进行约束，一般是根据经济理论进行直观的判断，但是这种方法带有很强的主观色彩，缺乏科学依据（Norman和Granger，1994）。因此研究方法亟待改进，有向无环图（DAG）方法的出现很好地解决了这一问题。

（二）有向无环图（DAG）

其实在DAG方法出现以前，研究变量之间因果关系比较常用的方法是进行格兰杰因果关系检验。该方法是由英国著名经济学家格兰杰（Granger，1969）提出的。格兰杰非因果性检验指的是，若加上xt的滞后变量后对yt的预测精度不存在显著性改善，则称xt-1对yt存在格兰杰非因果性关系，为简便，通常把xt-1对yt存在非因果关系表述为xt对yt存在非因果关系（严格讲，这种表述是不正确的）。但是从定义上我们就可以发现格兰杰因果关系检验存在以下两个问题：一是格兰杰因果检验是检验统计上的时间先后顺序，并不表示这两个变量之间存在真正的因果关系，具体还要依据模型和经济理论进行解释（庞皓和陈述云，1999）；二是格兰杰的因果关系检验通常检验的是滞后期变量之间的相关关系，无法检验当期因果关系。

正是基于此，Pearl（1995）和Hoover（2003）等提出了有向无环图（directed acycline graph）的方法，可以用于分析变量之间的当期因果关系。该方法是通过分析扰动项无条件相关系数和偏相关系数（条件相关系数）之间的关系来确定变量之间的当期因果关系。检验过程如下：(www.daowen.com)

步骤1：建立相关性关系的原假设。首先建立无向完全图，即变量之间通过无方向的线连接在一起，假设变量之间存在着同期的因果关系。

步骤2：运用PC算法对变量之间的关系进行筛选分析。首先通过回归残差的相关系数矩阵进行第一次筛选测算，如果变量之间的相关关系没有通过显著性检验，则删掉变量之间的连线，说明变量之间不存在同期因果关系。其次运用回归残差的偏相关系数进行第二次筛选测算，如果相关关系没有通过显著性检验则删掉。以此类推，直至进行第N-2阶偏相关系数显著性检验。在整体相关性检验中，经常使用的是Fisher提出的Z统计检验量（Awokuse，2003），该检验表达式如下所示：

其中ρ（i，j|k）表示以k个变量为条件的变量i和变量j之间的总体相关系数，n表示样本量。

步骤3：识别变量之间因果关系的方向。关于因果关系方向的识别，运用的是相邻集和隔离集的概念。在无向完全图中，如果经过删边后两个变量之间仍然保留连接线，表明两个变量之间存在相关关系，并且变量之间是相邻的，如X-Y。如果三个变量之间存在如下关系X-Y-Z，且以Y为条件的X与Z偏相关系数为0，则说明变量Y是变量X与变量Z的隔离集。即ρ（X，Z|Y）=0。给出以上定义以后，我们有如下推论：当无向完全图为X-Y-Z，X与Y相邻，Y与Z相邻，但是X与Z不相邻，如果Y不是X与Z隔离集，那么三个变量之间的相关关系方向为X→Y←Z；当无向完全图为X-Y-Z，X与Y相邻，Y与Z相邻，但是X与Z不相邻，如果已知X→Y，那么Y与Z的同期因果关系为Y→Z（Johansen，1991；Yang等，2006）。

步骤4：结果解释。通过建立原假设，并运用PC算法删边和定向，最终我们可以得到变量之间的因果关系有向无环图。总结起来，变量之间一共存在以下几种情况：

步骤5：过度识别检验。在进行有向无环图DAG的分析后，我们需要运用sims（1986）提出的似然比检验方法，对DAG的分析结果进行检验。检验方法如下：

其中，det代表对矩阵求行列式，ln表示对结果取对数，cov1代表约束条件下残差协方差矩阵，cov2代表无约束条件下残差协方差矩阵。LM服从自由度为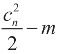（）的卡方分布，其中n表示内生变量个数，m为约束条件个数。

与以往通过经验判断决定SVAR模型结构式的约束不同，有向无环图基于扰动项的相关系数和偏相关系数的检验，避开了经验分析的主观性，确保了SVAR模型后续研究的科学性和合理性。