对于简单随机抽样，总体均值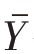与总体总值Y的线性回归估计量定义为

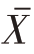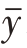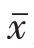估计量右下角的“lr”取自linear regression（线性回归）。其中，已知，、是样本均值，β可以是事先设定的常数，也可以是从样本中计算得到的某一特定的统计量，例如样本回归系数。β一旦确定，回归估计量的形式也就确定了。

特别地，当β=0时，，所以简单估计量和比率估计量都可以看成是回归估计量的特例；当β=1时，实质是用

（一）β为预先设定时的情形

β为事先设定时的回归估计量，理论简单又富有启发性。在实际问题中，也常常可以将β事先确定，例如，为同样目的进行的调查若重复多次，则有理由将从以往的资料中得出Yi对Xi的回归系数B作为β的设定值。此时，回归估计量为

在简单随机抽样中，当β=B事先设定时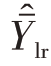，是的无偏估计量。其方差为

当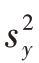、、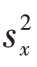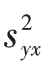分别为简单随机样本的方差与协方差时，则方差V 的无偏估计量为

以上对y与x的关系未作任何假定，不论y与x有何种关系，不论B取什么值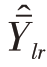，总是无偏的，但方差的大小会受到B的影响。那么B的最佳值应该为多少？显然B的最佳值实际上就是使估计量的方差达到极小时的取值。可以证明当

时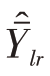，的方差达到极小，且

其中，ρ为Y与X的总体相关系数。

证明：要使V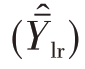为极小值，则由V 对B的偏导数等于零，即

可得

则由式（4.44）可得

（二）β需从样本计算时的情形(www.daowen.com)

当β需从样本计算时，受前面确定B最佳值的思路的启发，β的一个有效估计应是总体回归系数的最小二乘估计，也即取β为样本回归系数b，则

此时，总体均值的回归估计量为

这时的回归估计量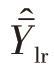与β=B时不同，不再是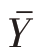的无偏估计量，而是近似无偏的，因为样本回归系数本身是一个随机变量，是总体回归系数的估计量。

在简单随机抽样中，当n足够大时，有

方差的估计量为

式中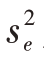，为样本残差方差，可表示为

例4.3　（续例4.1）为估计某县小麦总产量，在全县N=576个村中抽取n=24个村的简单随机样本，根据原始数据以及例4.1中已计算过的中间结果，可得

样本回归系数：

残差方差：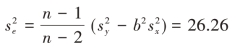

于是总产量Y的回归估计为

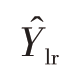的方差估计为

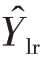的标准差估计为

例4.1　中已计算得=620.53（吨），=3837.87（吨），显然比率估计与回归估计都比简单估计精确得多，而回归估计与比率估计的精度差别不是很大，前者稍好一些。